作者：披头与枪花
https://zhuanlan.zhihu.com/p/1968757538867647052

《Defeating the Training-Inference Mismatch via FP16》
https://arxiv.org/pdf/2510.26788

这篇论文直指当前 LLM 强化学习（RL）微调中一个“老大难”问题——训练不稳定。你可能也遇到过，RLHF（基于人类反馈的强化学习）的训练过程极其脆弱，经常莫名其妙就“崩了”。

过去，我们普遍认为这是算法设计、超参设置或工程实现的问题。而这篇论文提出了一个颠覆性但又极其简单的观点：问题的根源，可能就是你习以为常的 BF16 浮点数精度！

作者证明，仅仅是将训练精度从 BF16 切换到 FP16，就能“奇迹般”地解决这个不匹配问题，带来更稳定的训练、更快的收敛和更强的最终性能。

主要目录

问题的核心：什么是“训练-推理不匹配”？
现有的（有缺陷的）解决方案
真正的“元凶”：为什么 BF16 是问题所在？
眼见为实：离线分析与可视化
一个更干净的“靶场”：作者提出的“理智测试”
关键实验：FP16 如何“吊打”所有 BF16 算法？
普适性验证：MoE、LoRA 和大模型都适用吗？
结论

1. 问题的核心：什么是“训练-推理不匹配”？

在对 LLM 进行强化学习微调时（例如 PPO 算法），我们通常需要两个组件：

1.Inference Engine（推理引擎）：用于快速生成“经验”（Rollout）。它会用当前模型策略，针对一批提示（prompt）生成回答（response）。

2.Training Engine（训练引擎）：用于计算梯度并更新模型参数。

为了追求极致的系统效率，现代 RL 框架（如 VeRL, Oat）会为这两个组件使用不同的计算引擎。例如，推理可能使用 vLLM 这样高度优化的引擎，而训练则使用 DeepSpeed 或 FSDP。

这就是问题的开端。

尽管这两个引擎在数学上是等价的（都代表同一个模型），但由于各自的实现、硬件优化和并行策略不同，它们在计算浮点数时会产生微小的数值差异（即精度误差）。

当模型使用 BF16 这样低精度格式时，这些微小的舍入误差在 token 自动回归生成（autoregressive sampling）的过程中会不断累积。一个 token 的微小差异，会导致下一个 token 的选择完全不同，最终导致推理策略（我们称之为 \mu）和训练策略（我们称之为 \pi）产生显著的分歧。

这种 \mu \neq \pi 的情况，被称为“训练-推理不匹配”（Training-Inference Mismatch）。

它会导致两大灾难性后果：

1.Biased Gradient（有偏梯度）：我们的经验数据是 y \sim \mu（从推理引擎采样），但我们计算梯度时用的却是 \nabla_{\theta} \log \pi(y|x)（训练引擎的概率）。当 \mu \neq \pi 时，这个梯度的期望值不再是真实梯度的无偏估计，导致优化走向错误的方向。

2.Deployment Gap（部署鸿沟）：我们的目标是优化在部署时（使用推理引擎 \mu）的表现，但我们实际上优化的却是训练引擎 \pi。这两个目标的不一致，导致模型在训练时“看起来很好”，但一部署，性能就下降。

2.现有的（有缺陷的）解决方案

为了解决这个 mismatch，学术界和工业界主要尝试了两种方法：

(1) 算法“打补丁”：重要性采样 (IS)

既然 \mu 和 \pi 不一样，熟悉强化学习的同学会立刻想到用重要性采样 (Importance Sampling) 来修正。

其核心思想是给梯度乘以一个修正系数（即概率比值 \frac{\pi(y|x)}{\mu(y|x)}），从而得到一个无偏的梯度估计。

\nabla_{\theta}\mathcal{J}_{pg.is}(x) = \mathbb{E}_{y \sim \mu(\cdot|x,\theta')} \left[ \frac{\pi(y|x,\theta)}{\mu(y|x,\theta')} \nabla_{\theta} \log \pi(y|x,\theta) \cdot A(x,y) \right]

公式含义：这是标准的基于重要性采样的策略梯度。我们从推理策略 \mu 采样 y，然后用概率比值 \frac{\pi}{\mu} 来修正 \log \pi 这一项，使其在期望上等于从 \pi 采样的结果。A(x,y) 是优势函数。

这个方法理论很美，但实践中很糟：

高方差：对于 LLM 生成的长序列，y 的概率是所有 token 概率的连乘积。\pi 和 \mu 之间的微小差异在连乘后会被指数级放大，导致 \frac{\pi}{\mu} 这个比值要么接近 0，要么变得极大。这带来了巨大的方差，训练极其缓慢且不稳定。

为了缓解高方差，后续工作提出了“妥协”方案，如 TIS（截断IS）和 MIS（掩码IS），通过裁剪 (clipping) 概率比值来牺牲一定的无偏性以换取稳定性。

但所有这些算法“补丁”都有两个根本缺陷：

1.计算昂贵：为了计算 \frac{\pi(y|x)}{\mu(y|x)}，你需要用两个引擎（或一个引擎跑两次）分别计算一遍完整序列的概率，这额外增加了约 25% 的训练开销。

2.治标不治本：它没有解决“部署鸿沟”。它只是强行让 \pi 的训练去拟合 \mu 的采样，但最终得到的模型参数 \theta 仍然是 \pi 上的最优解，而不是 \mu 上的。

(2) 工程“对齐”

另一条路是花大力气去手动“对齐”训练和推理引擎的实现细节，比如统一 CUDA kernel、统一并行策略等。但这需要深厚的领域知识和巨大的工程努力，且非常“脆弱”，换个框架或模型就得重来。

3.真正的“元凶”：为什么 BF16 是问题所在？

这篇论文的作者另辟蹊径，他们发现上述努力都“搞错了方向”。问题的根源不在于算法，而在于我们使用的浮点数精度。罪魁祸首就是 BF16 (BFloat16)。

为什么我们会用 BF16？ BF16 被 Google 推出并成为现代 LLM 预训练的“标配”，是因为它有 8 个指数位，动态范围和 FP32 完全一样。这使得它在预训练时能很好地处理极大或极小的梯度值，几乎不会发生溢出 (Overflow) 或下溢 (Underflow)，训练非常稳定，还不需要 FP16 时代繁琐的损失缩放 (Loss Scaling)。

但 BF16 的“阿喀琉斯之踵”在于它只有 7 个尾数位。这意味着它的数值精度极低。两个非常接近的数字，在 BF16 看来可能是完全一样的。

这正是“训练-推理不匹配”的根源！

因为 BF16 精度太低，训练引擎和推理引擎各自不同的实现方式（如不同的 CUDA kernel）所引入的舍入误差 (Rounding Errors) 会非常大。这些巨大的误差在序列生成中不断累积，最终导致了 \pi 和 \mu 的显著偏离。

而 FP16 恰恰相反： FP16 有 10 个尾数位，其精度是 BF16 的 2^{(10-7)} = 2^3 = 8 倍！

核心洞察：在 RL 微调阶段，模型的权重和激活值已经通过预训练稳定在一个合理的范围内，BF16 的“超大动态范围”不再是刚需。相反，由 BF16 的“超低精度”所导致的舍入误差，成为了稳定性的致命伤。

切换到 FP16，凭借其高 8 倍的精度，训练引擎和推理引擎的计算结果在数值上几乎完全一致。这从根本上消除了 \pi 和 \mu 发生偏离的可能性。

那 FP16 的动态范围小怎么办？ 作者指出，这在早期是一个问题，但现在已经是一个 “已解决的问题”。我们只需启用现代训练框架（如 PyTorch）中内置的动态损失缩放 (Dynamic Loss Scaling) 即可。它会自动放大 Loss 来防止梯度下溢，并在发生溢出时自动缩小 scale，非常成熟且开销极小。

4.眼见为实：离线分析与可视化

作者首先做了一个离线实验来验证他们的猜想。

他们让模型在 BF16 和 FP16 两种精度下，分别用推理引擎 (\mu) 和训练引擎 (\pi) 对同一批数据计算概率。

结果一目了然 (见 Figure 2)：

Token 级概率 (左侧两图)：

BF16：散点图中的点弥散在对角线（y=x）周围，很多点的偏差都很大。
FP16：所有的点都完美地聚集在对角线上，说明 \pi 和 \mu 的计算结果几乎完全相同。

序列级不匹配 (右侧两图)：

BF16：随着序列长度 (Sequence length) 增加， log(\frac{\pi}{\mu}) 的误差（即不匹配程度）呈指数级增长（在 log 图上斜率 \approx -1.01）。
FP16：误差几乎为零，并且不随序列长度增加而累积（斜率 \approx -0.07）。

这个实验无可辩驳地证明了：训练-推理不匹配，本质上是 BF16 低精度导致的数值问题。而 FP16 几乎没有这个问题。

5. 一个更干净的“靶场”：作者提出的“理智测试”

标准 benchmark（如 MATH）太“脏”了，它混杂了模型“闭着眼都能做对”的简单题和“打死也做不对”的难题。在这样的数据集上，算法跑崩了，你很难判断是算法不行，还是模型本身的能力局限。

为此，作者设计了一个 “理智测试” (Sanity Test)：

数据集构建：他们从 MATH 数据集里，筛选出那些初始模型（DeepSeek-R1-Distill-Qwen-1.5B）正确率在 20% 到 80% 之间的题目。
含义：这个“完美数据集”(perfectible dataset) 中的题目，都是模型“踮踮脚就能够到”的，既非 trivial 也非 impossible。
测试标准：一个稳定可靠的 RL 算法，理应能在这个数据集上通过训练，达到接近 100% 的训练准确率。如果达不到，就说明这个算法本身设计或实现有缺陷。

这个“理智测试”为评估 RL 算法的稳定性提供了一个干净、高效的“靶场”。

6.关键实验：FP16 如何“吊打”所有 BF16 算法？

有了“理智测试”这个靶场，作者开始了一场“大比武”。

(1) 实验设置

框架： VeRL 和 Oat（两种主流 RL 框架，用于交叉验证）
模型： DeepSeek-R1-Distill-Qwen-1.5B
BF16 组（对照组）：

BF16 GRPO (普通 GRPO)
BF16 GRPO-Token-TIS (带 Token 级 TIS 补丁)
BF16 GRPO-Seq-MIS (带 Sequence 级 MIS 补丁)
BF16 GSPO

FP16 组（实验组）：

FP16 PG-Seq-IS (最简单、最原始的重要性采样策略梯度)

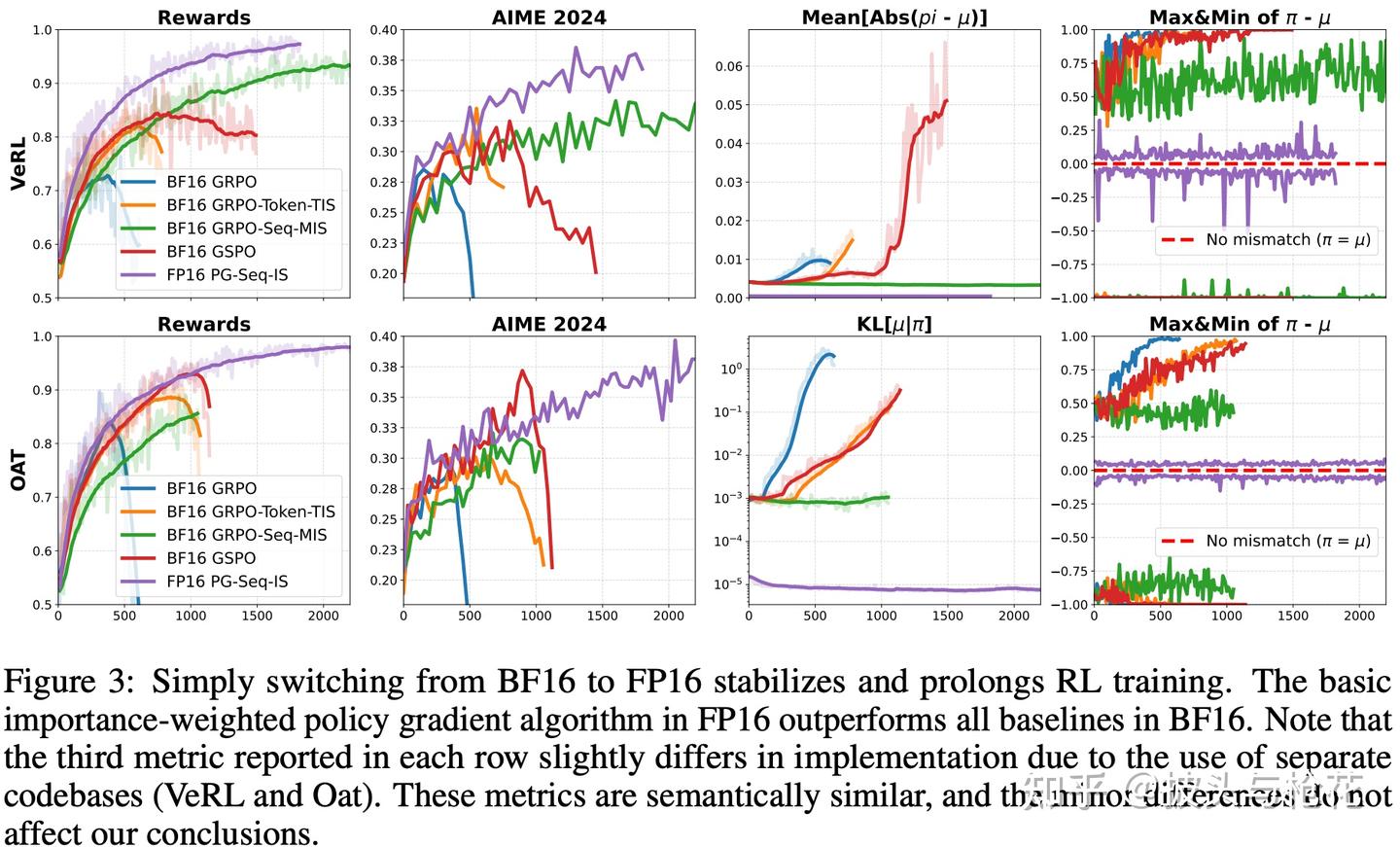
(2) 实验结果 (见 Figure 3)

BF16 组（蓝/橙/红线）：

BF16 GRPO (蓝色) 和 BF16 GRPO-Token-TIS (橙色) 全部提前崩溃 (Collapse)！训练奖励上升一段后就急转直下。
BF16 GRPO-Seq-MIS (红色) 是 BF16 组里唯一保持稳定的。但它的收敛速度极慢，并且最终收敛到的奖励值（约 95%）显著低于 FP16 组（约 99%）。——这就是“部署鸿沟”的体现，即使稳定，它也达不到最优性能。
FP16 组（紫色线）：
FP16 PG-Seq-IS (紫色) 使用的是最简单的标准算法，但它的表现是压倒性的：
完全稳定，全程没有崩溃。
收敛最快，甩开所有 BF16 组。
性能最强，达到了近 100% 的训练奖励。

这个结果说明：与其在 BF16 上费尽心机地设计复杂的算法补丁（TIS/MIS），不如直接切换到 FP16，用最简单的算法反而能获得最好的效果。

(3) FP16 下的算法对比 (见 Figure 4)

作者还做了一个实验：在 FP16 精度下，跑一遍所有的算法 (GRPO, TIS, MIS, ...)

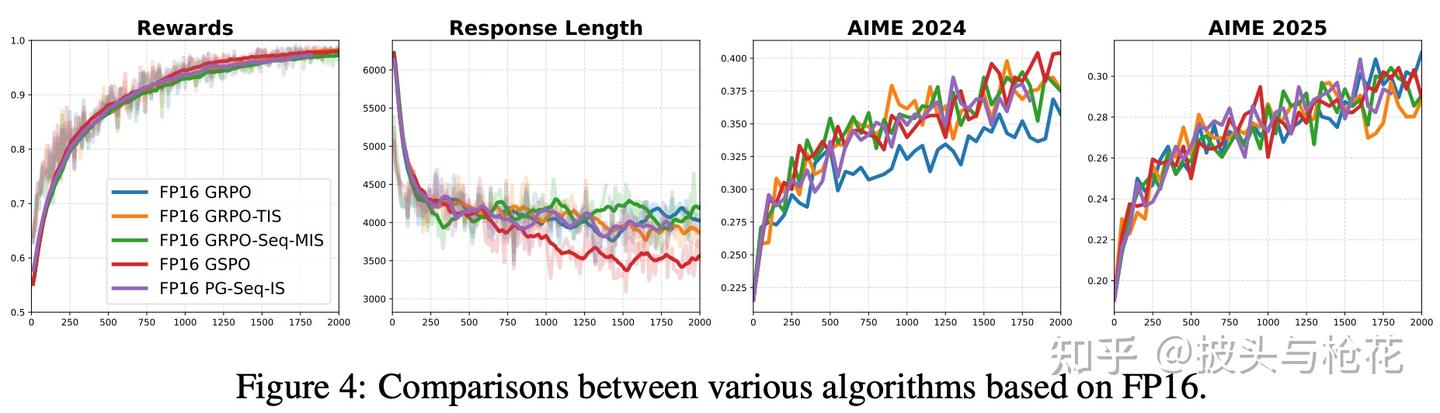
结果发现：一旦使用了 FP16，所有算法的表现都变得几乎一模一样，全都又快又好。

洞察：这说明 TIS, MIS 这些复杂的“补丁”之所以存在，唯一的原因就是为了缓解 BF16 带来的 mismatch。当 FP16 从根源上消除了 mismatch 后，这些补丁就变得毫无意义了。

(4) 精度组合的消融实验 (见 Figure 5)

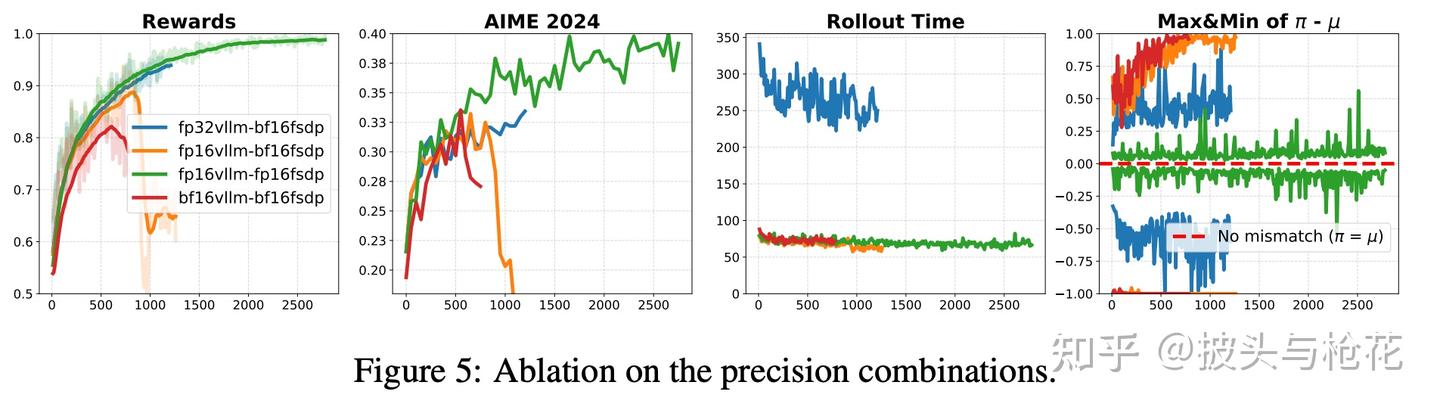
作者还探索了不同的训练/推理精度组合：

BF16(训) - BF16(推)：崩溃。
BF16(训) - FP16(推)：崩溃（稍晚）。
BF16(训) - FP32(推)：稳定了！但推理速度慢了 3 倍，完全不实用。
FP16(训) - FP16(推)：完美。既完全稳定，又保持了最快的速度和最高的性能。

结论： FP16(训) + FP16(推) 是兼顾稳定性、效率和性能的最优组合。

7. 普适性验证：MoE、LoRA 和大模型都适用吗？

为了证明这个结论不是巧合，作者在更广泛的场景下进行了验证（见 Figure 1，即首页的 12 宫格图）。

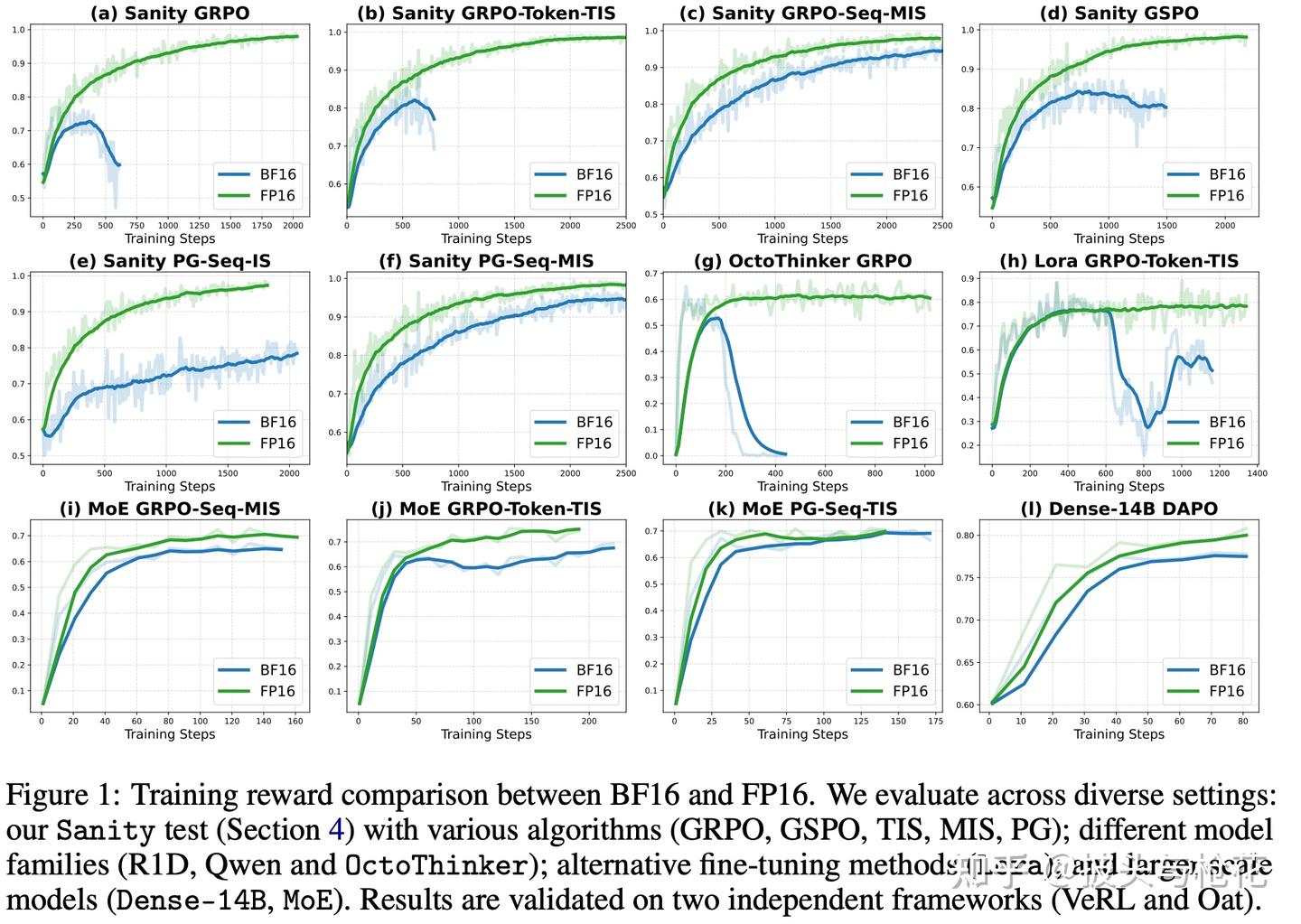
1.MoE RL (图 i, j, k)： MoE 模型的 mismatch 问题更严重。实验显示，FP16（绿线）的稳定性、收敛速度和最终奖励全面优于 BF16（蓝线）。

2.LoRA RL (图 h)：在 LoRA 微调中，BF16（蓝线）训练发生严重崩溃，而 FP16（绿线）全程保持稳定。

3.Large Dense Models (图 l, Dense-14B)：在 14B 的大模型上，FP16（绿线）的收敛速度和最终性能也明显快于和高于 BF16（蓝线）。

4.Other Model Families (图 g, OctoThinker)：换成 Llama 系的底座模型，BF16（蓝线）依然崩溃，而 FP16（绿线）依然稳定。

所有实验都指向同一个结论：FP16 带来的好处是普适的。

8. 结论

这篇论文的结论清晰而有力：

1.LLM 的 RL 微调不稳定的主要“元凶”之一，是 BF16 的低精度所导致的“训练-推理不匹配”。

2.BF16 的低精度（7 尾数位）导致舍入误差累积，使训练和推理策略发生偏离。

3.现有的算法补丁（TIS/MIS）计算昂贵、治标不治本，且无法解决“部署鸿沟”。

4.一个极其简单且高效的解决方案是：切换到 FP16 精度（配合动态损失缩放）。

5.FP16 凭借其高 8 倍的精度（10 尾数位），极大的缓和了数值不匹配的现象，使得最简单的 RL 算法也能变得极其稳定、收敛更快、性能更强。

这篇文章是工程实践与科研洞察完美结合的典范。它提醒我们，在埋头改进复杂算法（如各种 IS 变体）之前，或许应该先退一步，审视一下我们技术栈中最基础的假设——比如，“BF16 是 LLM 训练的标配”。

对于 RL 微调这个特定阶段，精度（FP16）的重要性，可能已经压倒了动态范围（BF16）。

给实践者的建议： 如果你正在被 RLHF 的训练稳定性所困扰，不要犹豫，立刻试试将你的训练框架切换到 FP16 + Dynamic Loss Scaling。这几行代码的改动，可能比你花几周时间去调算法、调超参要有效得多。