作者：Lancer
https://zhuanlan.zhihu.com/p/1969465397670551963

一、 为什么需要mxfp8、mxfp4、nvfp4等低精度格式？

1.大模型规模爆炸式增长 → 计算与内存瓶颈加剧

• LLM 参数量已达万亿级别，训练 FLOPs 超 10²⁵。
• 传统 FP32/BF16 格式占用高带宽内存，限制吞吐和能效。
• 单纯降低位宽（如 INT8/FP8）会导致动态范围不足，引发训练发散或精度下降。

2.传统低精度格式存在固有缺陷

• INT8：需要预设 scale，无法适应 LLM 中幂律分布的 activations/gradients（含大量 outlier），易 clipping。
• 标准 FP8（如 E4M3/E5M2）：虽为浮点，但若对整个tensor使用单一scale（per-tensor scaling），仍无法兼顾块内大值与小值，导致量化误差。

为此，提出MX（Microscaling）低精度格式，它是 “块共享 scale + 低精度元素” 的混合表示，其基本结构如下：

1 个共享 scale：E8M0（8-bit exponent-only，power-of-2）

32 个低精度元素：FP8 / FP6 / FP4 / INT8

NVFP4 是 MX 思想的 NVIDIA 工程增强版：

• 继承了“块共享 scale + 低精度元素”的核心范式；
• 但通过 更小块（每块16 元素） + 更精确 scale（E4M3）等，解决了 MXFP4 在 4-bit 下的数值瓶颈（受限于 scale 的离散性（只能是 2ⁿ），导致无法将原始数据最优压缩到 FP4 的完整表示区间，造成有效精度和动态范围的浪费）。

总体来说，MX/NVFP 格式通过“块共享 scale + 低精度元素” 的混合表示，在 4–8 bit 下实现“高动态范围 + 高数值稳定性 + 高硬件效率”的统一解决方案，是 LLM 大规模训练可持续发展的关键技术路径。

二、mxfp8、mxfp4、nvfp4介绍

mxfp8、mxfp4、nvfp4均为量化格式，相较于作为基准的bf16格式，具有存储占用更小、计算速度更快的性能优势，但在转换过程中会存在一定的转换开销和精度损失，实际性能取决于 GEMM 尺寸（MKN） 和 量化开销融合程度。本文中没有涉及到mxfp6（E3M2/E2M3），其动态范围和精度介于 mxfp4 与 mxfp8之间，看了最新原生代码，没有发现相应的实现。

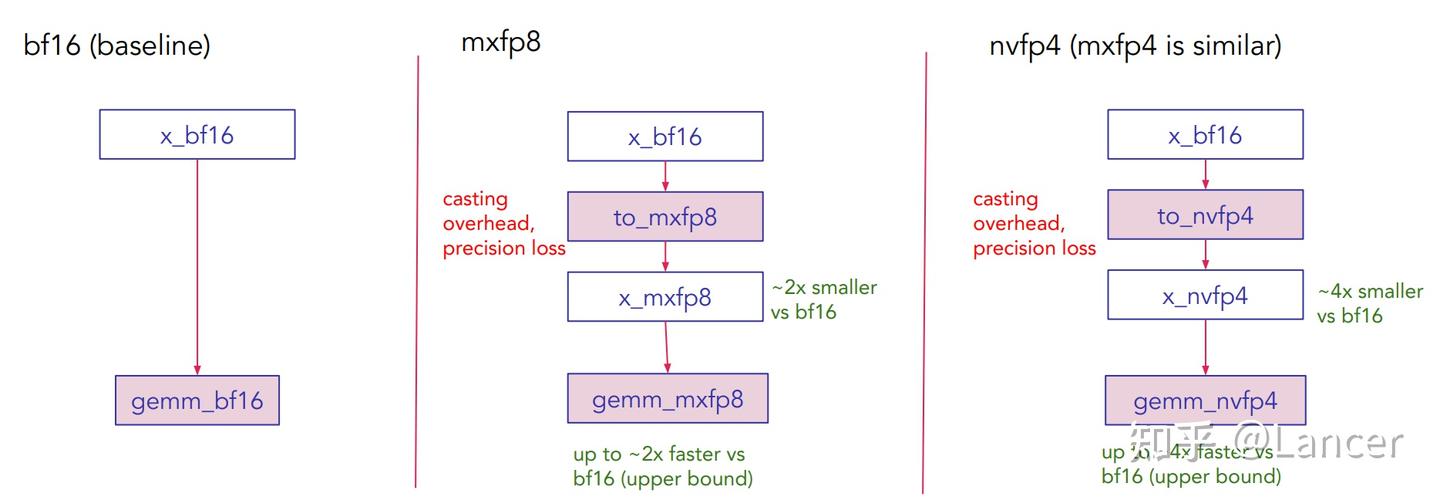
mxfp8 & mxfp4是OCP（Open Compute Project）定义的标准格式，AMD MI350x 和Blackwell支持；nvfp4是 NVIDIA 自研的格式，仅在其 Blackwell 架构上原生支持，旨在提供比标准 MX 格式更好的数值表现。NVIDIA之前的论文有提到，在 10 万亿 token 的超长训练周期下，它们使用 NVFP4成功训练 12B 参数的 LLM，训练损失能高度对齐 FP8，下游任务性能几乎无损，如下图所示。

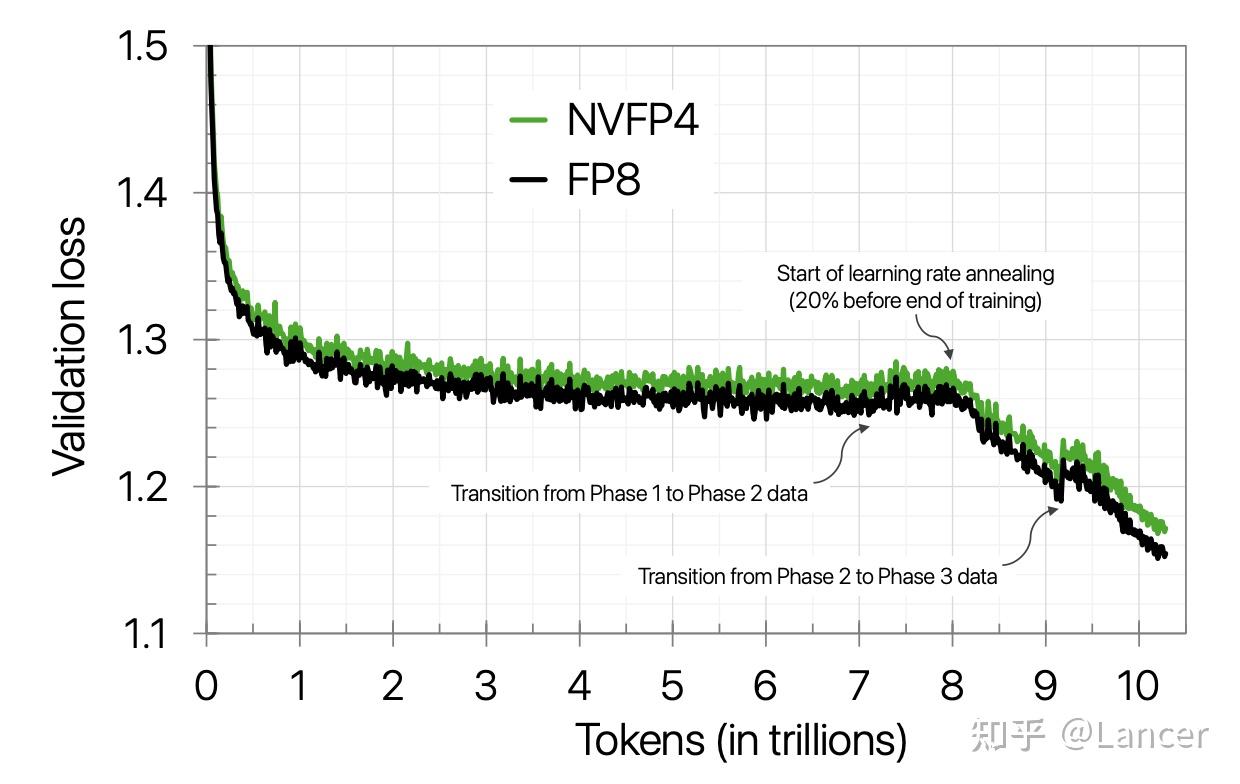
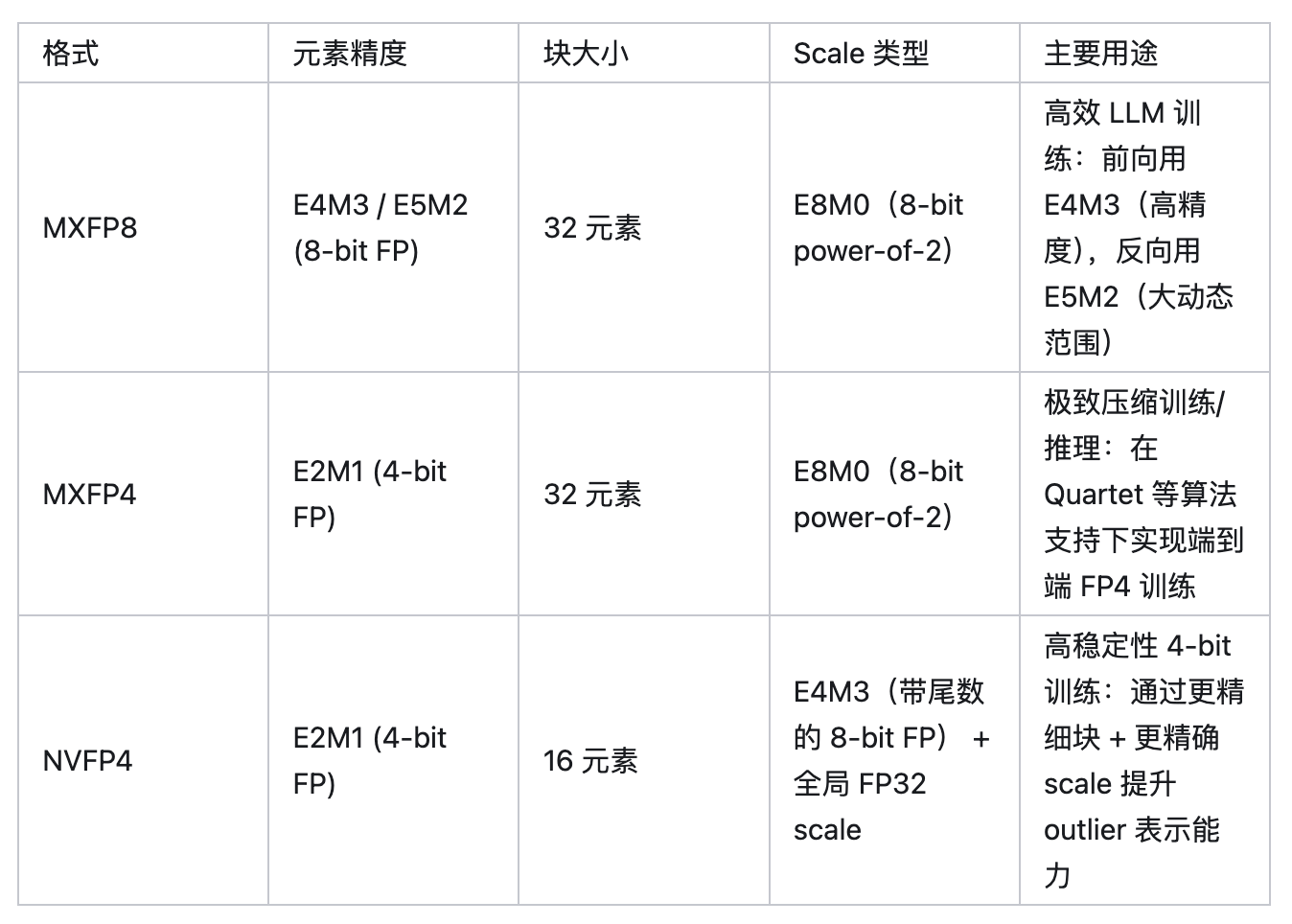
三、PyTorch中的微缩放格式：核心参数对比

针对4096×4096大小的bf16张量，mxfp8、mxfp4、nvfp4在PyTorch中的核心技术参数如下表所示：

四、微缩放格式的构建模块

mxfp8、mxfp4、nvfp4的构建模块原理相似，此处以mxfp8的GEMM（通用矩阵乘法）构建为例，核心包括新增数据类型、新增缩放方式和新增GEMM计算三部分，流程为：

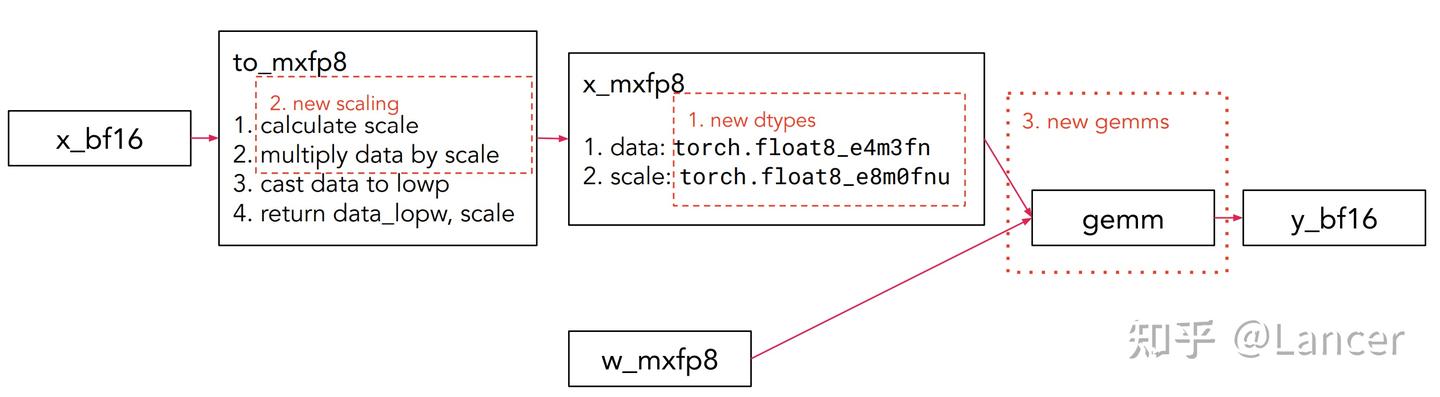
具体流程如下：

bf16格式数据（x_bf16）→ 经新增缩放方式和数据类型处理 → mxfp8格式数据（x_mxfp8）→ 参与新增GEMM计算 → 输出bf16格式结果（y_bf16），同时权重（w）也需转换为mxfp8格式（w_mxfp8）参与计算。

（一）数据类型

1.torch.float8_e8m0fnu

用途：mxfp8和mxfp4格式的缩放数据类型，用于存储torch.float32（单精度浮点数）的无符号指数。

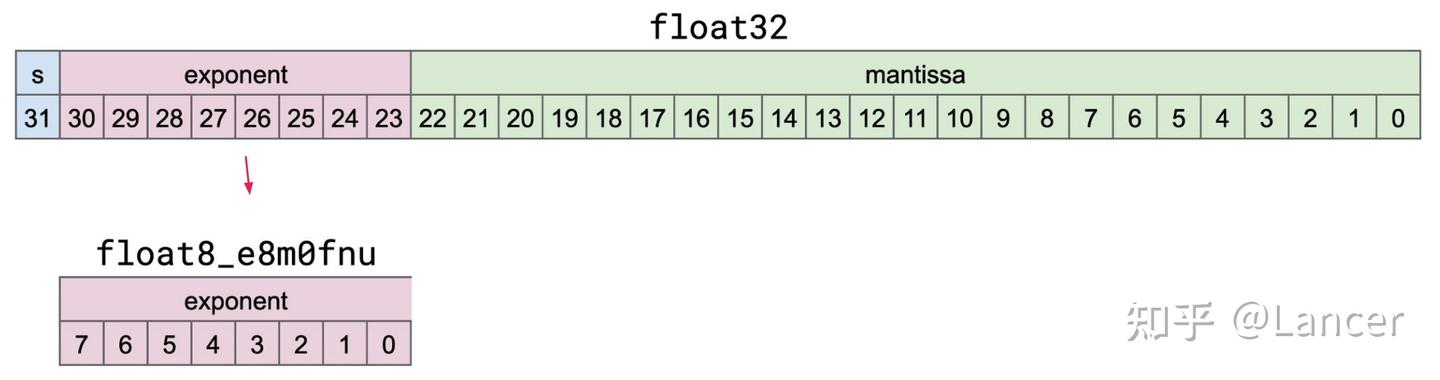
格式结构：共8位，仅包含指数位（0-7位），无尾数位，具体对应关系可参考float32的位结构（float32含符号位、指数位和尾数位，而该类型仅提取并存储无符号指数）。

后缀含义：“f”代表有限值（finite）、“n”代表非标准非数值（nonstandard NaN）、“u”代表无符号（unsigned）。

版本支持：在PyTorch 2.7.0及以上版本可用。

操作支持：

• 支持操作：创建（empty空张量、fill填充、zeros零张量）、字节级数据移动（cat拼接、torch.view视图转换、torch.reshape重塑）、类型转换、作为scaled_mm（缩放矩阵乘法）中mxfp8和mxfp4的缩放数据类型。
  不支持操作：大多数其他运算。

补充参数：

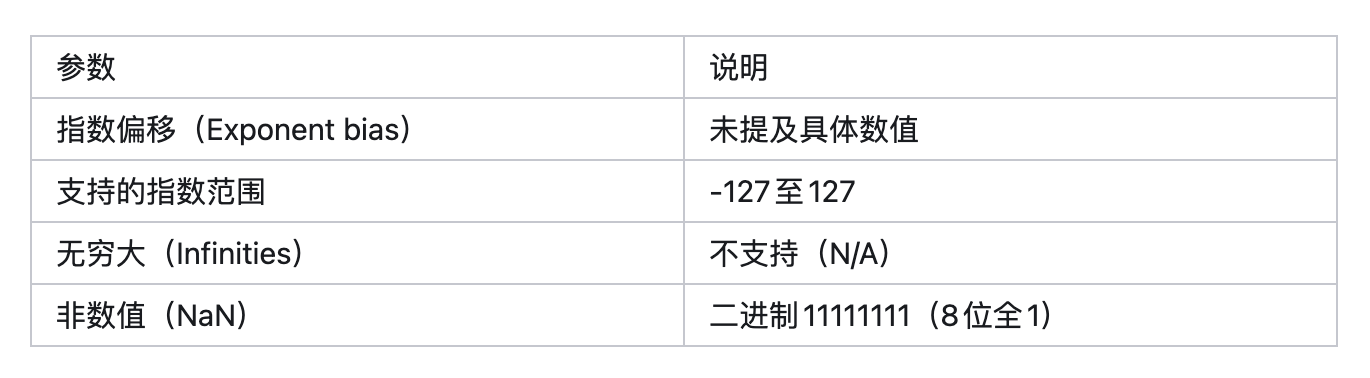
2.torch.float8_e4m3fn

用途：mxfp8格式的元素数据类型，是一种8位浮点数格式。

格式结构：共8位，包含1位符号位（S）、4位指数位（e）和3位尾数位（m），用于存储具体的元素数值。

后缀含义：“f”代表有限值（finite）、“n”代表非标准非数值（nonstandard NaN）。

舍入方式：默认采用RTNE（Round to Nearest, Ties to Even，四舍五入到最近值， ties时向偶数舍入），这也是PyTorch的默认舍入方式。

3. torch.float4_e2m1fn_x2

用途：mxfp4和nvfp4格式的元素数据类型，将两个float4（4位浮点数）数据打包到1个字节（8位）中存储。

格式结构：1个字节（8位）分为两部分，每部分对应1个float4数据：
高4位（7-4位）：包含1位符号位（S，7位）、2位指数位（e，6-5位）、1位尾数位（m，4位）。
低4位（3-0位）：包含1位符号位（S，3位）、2位指数位（e，2-1位）、1位尾数位（m，0位）。

后缀含义：“f”代表有限值（finite）、“n”代表非标准非数值（nonstandard NaN）、“x2”代表1个字节中打包2个数据。

版本支持：在PyTorch 2.8.0及以上版本可用。

操作支持：

• 支持操作：创建（empty、fill、zeros）、字节级数据移动（cat、torch.view、torch.reshape）、作为scaled_mm中mxfp4和nvfp4的元素数据类型。
  不支持操作：大多数其他运算。

取值范围：每个float4仅有16种可能取值，分别为[0, 0.5, 1, 1.5, 2, 3, 4, 6, -0, -0.5, -1, -1.5, -2, -3, -4, -6]。

补充参数：

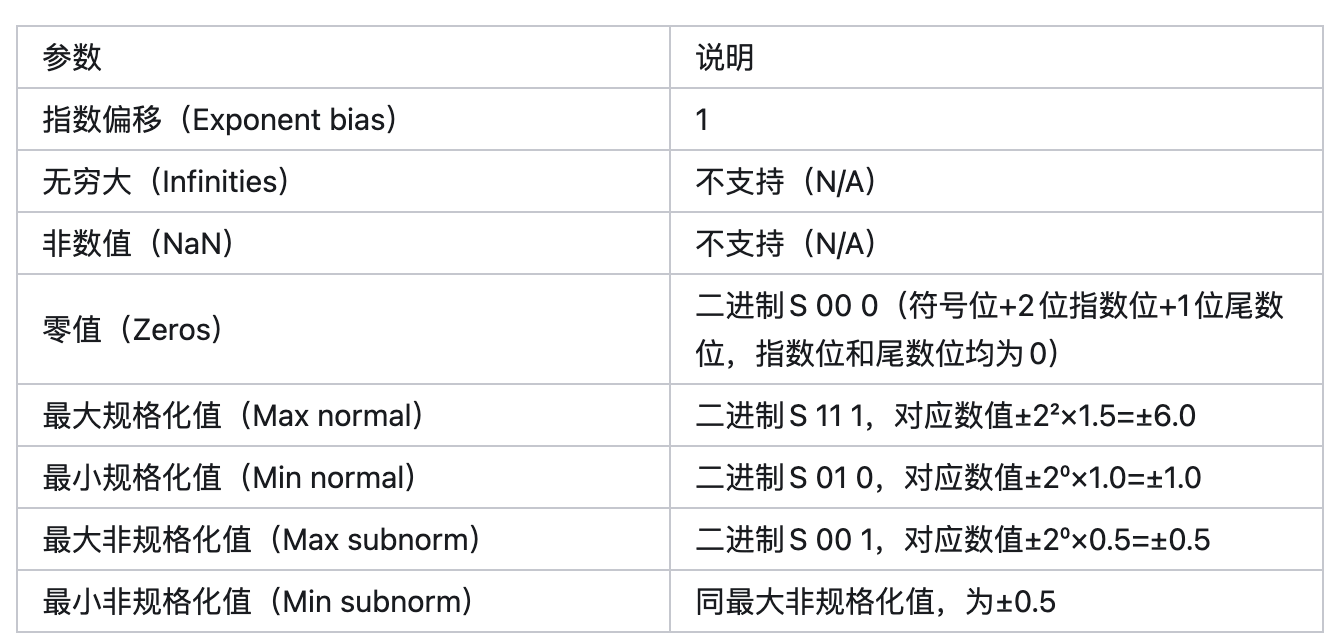
舍入方式：

• 默认采用RTNE，但目前在PyTorch中未对该类型开放此舍入方式的配置。
• 随机舍入（stochastic rounding）可用于提升训练数值稳定性；

（二）缩放方式

1.缩放的核心原理

浮点量化会将高精度张量（如FP64、FP32、FP16、BF16）存储为低精度张量（如FP8、FP4，即本文中的mxfp8、mxfp4、nvfp4），并搭配一个或多个缩放因子（scale）。选择缩放因子的目的是让高精度张量的数值范围与低精度张量的可用范围对齐，具体流程为：

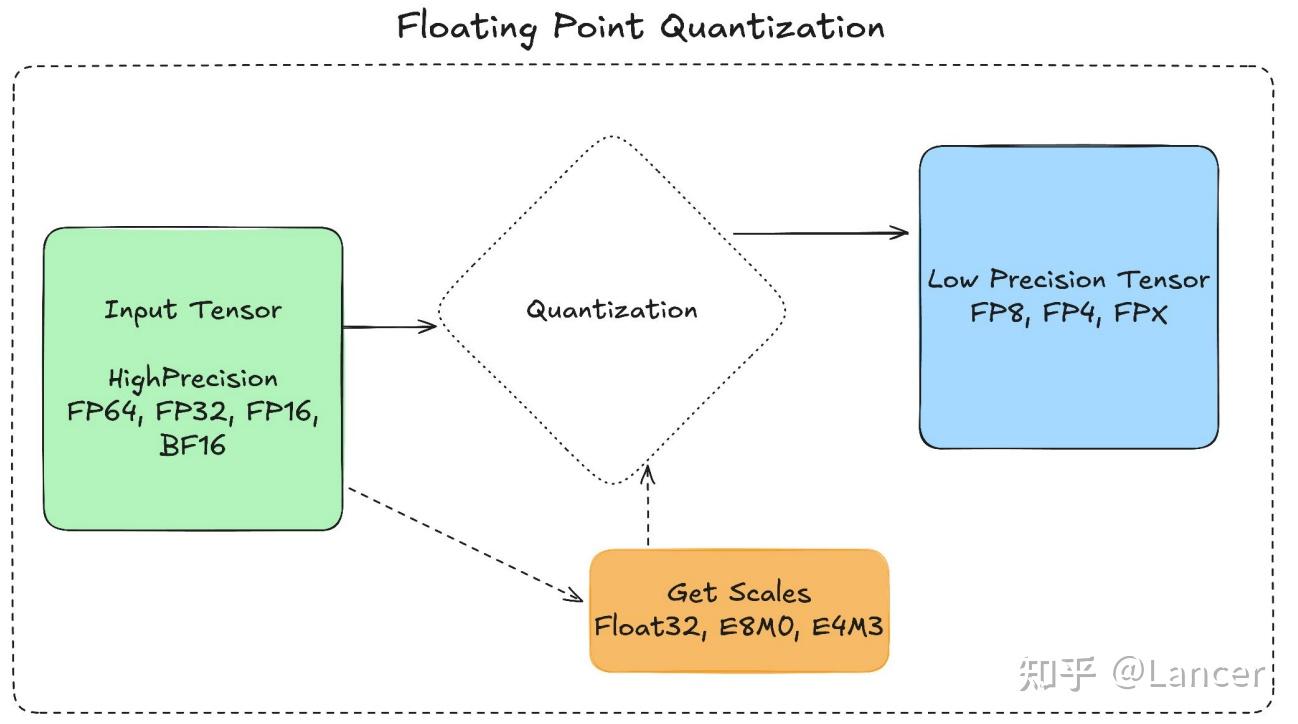
• 计算缩放因子，使高精度数据映射到低精度格式的有效范围内。
• 将高精度数据与缩放因子相乘后，直接转换（含截断处理）为低精度数据。
• 若需恢复原始数据，可将低精度数据转换回高精度格式后，乘以缩放因子的倒数（恢复过程会存在一定精度损失）。

2.为何需要缩放（而非直接转换）

如上图所示，直接将FP32转换为FP8（如mxfp8）会导致数据截断，产生巨大误差（最大误差可达352.00）；而先对数据进行缩放（如将FP32数据乘以0.56），再转换为FP8，可使数据完全落入FP8的有效范围，大幅降低转换误差。

3.主流缩放方案

不同硬件和模型场景下，采用的缩放方案（粒度、方式）不同，核心方案如下：

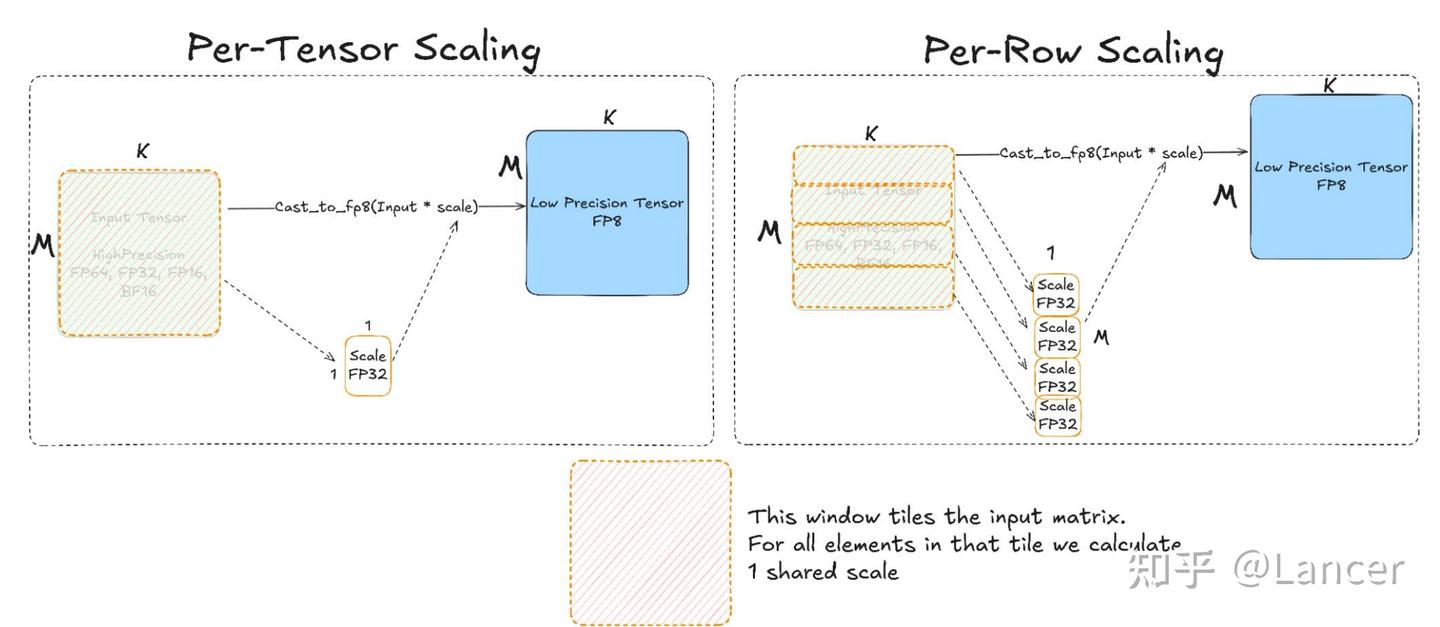
缩放方案	适用场景	核心逻辑
逐张量缩放（Per-Tensor Scaling）	Hopper、MI300等硬件	为整个输入矩阵计算1个全局缩放因子，将矩阵所有元素与该因子相乘后转换为低精度张量（如FP8）
逐行缩放（Per-Row Scaling）	Hopper、MI300等硬件	为输入矩阵的每一行计算1个缩放因子，每行元素分别与对应因子相乘后转换为低精度张量
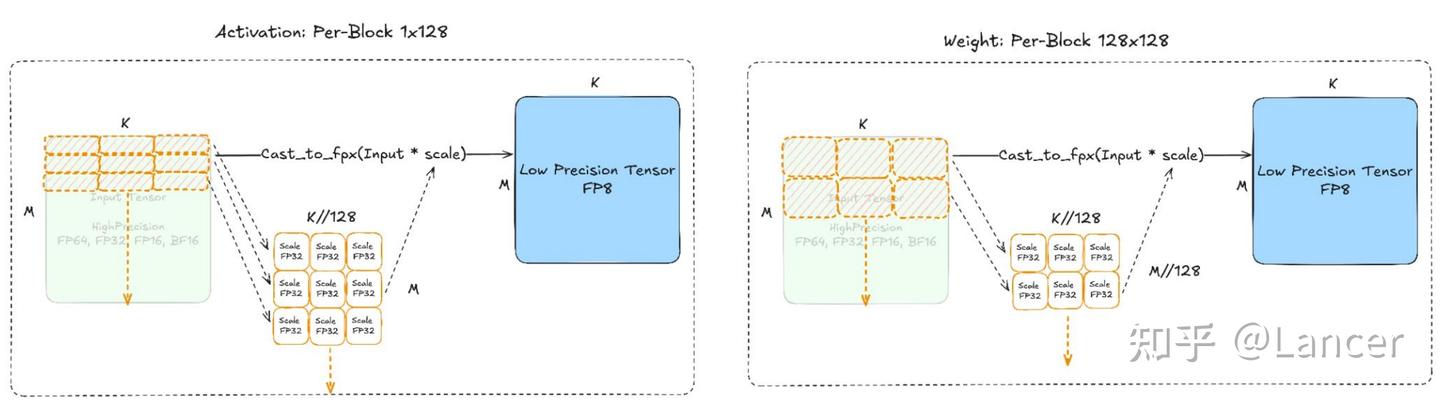
DeepSeekV3方案	DeepSeekV3模型	- 激活值（Activation）：采用1×128的块粒度缩放，即每1×128大小的块计算1个缩放因子。 - 权重（Weight）：采用128×128的块粒度缩放，即每128×128大小的块计算1个缩放因子
MX方案	mxfp8、mxfp4格式	- 缩放粒度：1×32（块大小），即每1×32大小的块计算1个缩放因子，相较于逐张量/逐行缩放，粒度更细，缩放因子更多。 - 缩放数据类型：采用E8M0（即torch.float8_e8m0fnu），支持2的幂次缩放
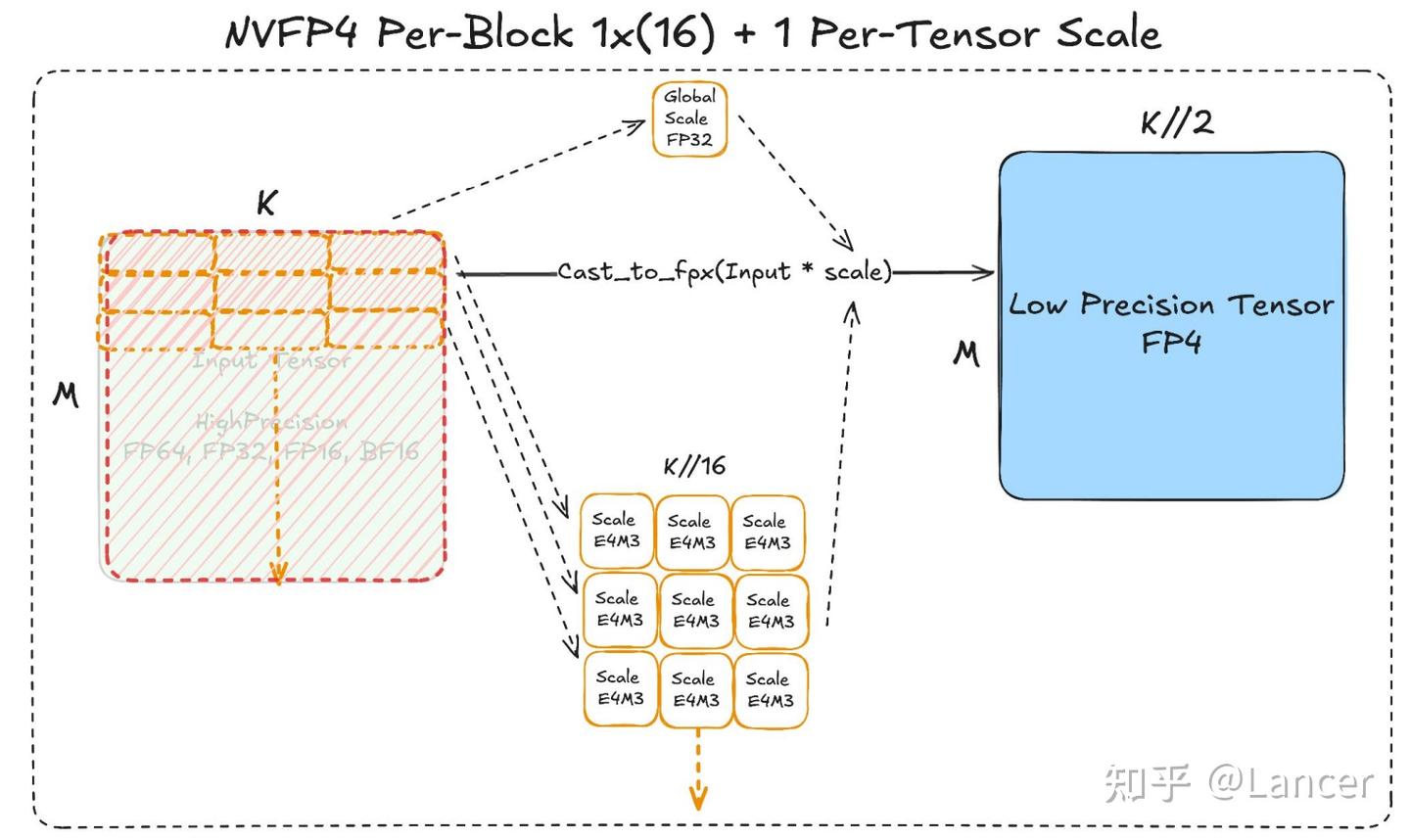
NVFP4方案	nvfp4格式	- 缩放粒度：1×16（块大小），粒度比MX方案更细，缩放因子更多。 - 缩放数据类型：采用E4M3（即torch.float8_e4m3fn），相较于E8M0，精度更高但数值范围更小。 - 额外处理：需1个全局FP32缩放因子，补偿E4M3缩放范围不足的问题

4.torch.float8_e8m0fnu的缩放计算模式

从数据的最大绝对值（max(abs(x))）计算E8M0（torch.float8_e8m0fnu）缩放因子的方式主要有两种：

• OCPMX规范（floor模式）：提取max(abs(x))的指数位，再减去元素数据类型的最大2次幂（elem_dtype_maxpow2），但是nvidia之前的论文有指出会导致部分值 溢出，因此提出向上取整的方法。
• NVIDIA （rceil模式）：将max(abs(x))除以元素数据类型的最大绝对值（max_abs_dtype），向上取整后，提取指数位。

（三）GEMM计算

GEMM计算（如mxfp8 GEMM、nvfp4 GEMM）的核心是基于低精度张量（mxfp8、nvfp4等）和对应的缩放因子，通过专用内核实现高效矩阵乘法，具体示例如下：

1.块缩放mxfp8 GEMM

# 1. 将输入张量A、B转换为mxfp8格式，同时得到对应的缩放因子A_scale、B_scale
A_scale, A_fp8 = to_mxfp8(A)
B_scale, B_fp8 = to_mxfp8(B)

# 2. 调用scaled_mm进行mxfp8格式的矩阵乘法
# scale_recipe_b指定B的缩放方案为1×32块粒度（Blockwise1x32）
# output_dtype指定输出结果为bf16格式
result = scaled_mm(A_fp8, B_fp8, 
                   scale_recipe_a=ScalingType.Blockwise1x32, 
                   scale_recipe_b=ScalingType.Blockwise1x32, 
                   output_dtype=torch.bfloat16)

其中，to_mxfp8（转换）、scaled_mm（缩放矩阵乘法）等函数和内核可在PyTorch的torch/ao模块中获取。

2.NVFP4块缩放GEMM

# 调用scaled_mm进行nvfp4格式的矩阵乘法
# scale_a指定A的缩放因子：1×16块粒度缩放因子（to_blocked(A.scales)） + 全局张量缩放因子（A_global）
# scale_recipe_a指定A的缩放方案：1×16块粒度（Blockwise1x16） + 张量级（TensorWise）
result = scaled_mm(A.fp.t(), B.fp, 
                   scale_a=[to_blocked(A.scales), A_global], 
                   scale_recipe_a=[ScalingType.Blockwise1x16, ScalingType.TensorWise],
                   # 其他参数根据实际需求配置
                   )

该计算支持多缩放因子和独立的内存重排模式，并可调度到专用内核（如cuBLAS、Cutlass、rocBLAS、Composable Kernel）执行。

五、性能表现

在NVIDIA B200 GPU上的测试结果显示，mxfp8和nvfp4相较于bf16，在GEMM计算性能上有显著优势，具体如下：

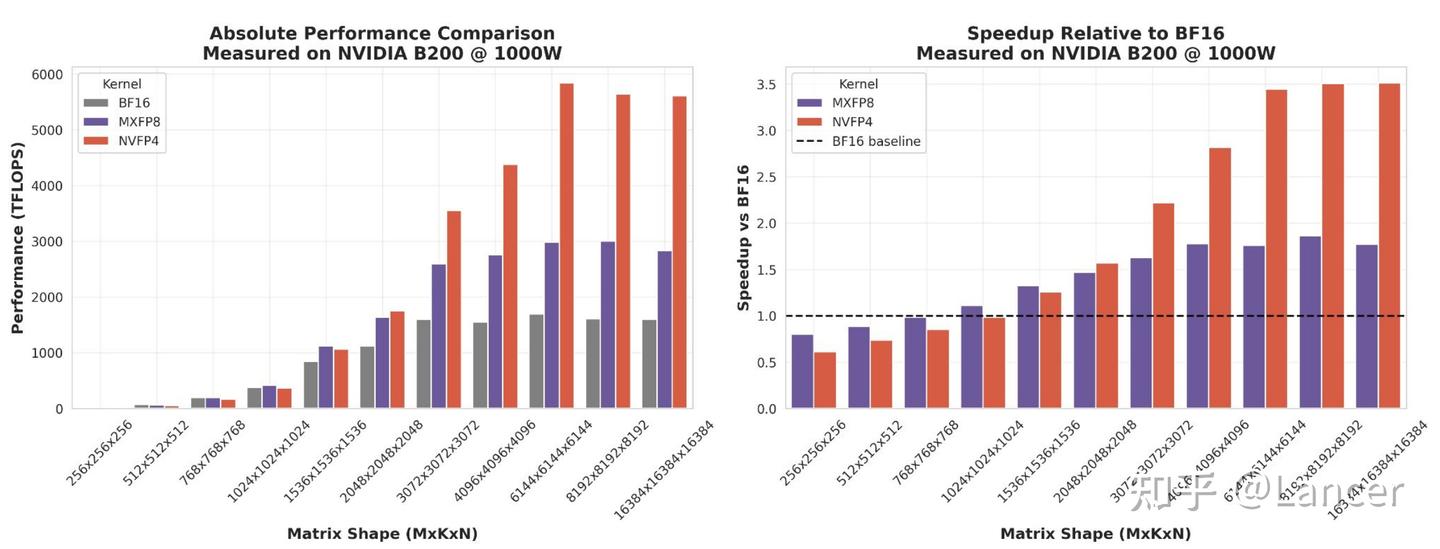
（一）绝对性能对比

随着矩阵尺寸（MxKxN）从256×256×256增大到16384×16384×16384，mxfp8和nvfp4的Kernel性能（逐渐超越bf16，且差距不断扩大。例如，当矩阵尺寸为16384×16384×16384时，nvfp4的性能接近6000 TFLOPS，mxfp8接近4000 TFLOPS，而bf16仅约2000 TFLOPS。

（二）相对性能对比（相较于bf16的加速比）

• 矩阵尺寸较小时（如256×256×256），mxfp8和nvfp4的加速比接近1（无明显优势），因此时缩放和转换的开销占比高。
• 随着矩阵尺寸增大（如超过2048×2048×2048），加速比逐渐提升：mxfp8的加速比最高接近2倍，nvfp4最高接近3.5倍，符合理论加速比预期（mxfp8最高2倍、nvfp4最高4倍）。

（三）缩放开销对比

不同缩放方案的开销不同，在相同矩阵尺寸下：

• 逐行缩放（per_row）和MX缩放的开销可通过1个内核完成，开销较低。
• 逐张量缩放（per_tensor）需多个内核协同，开销较高（如在16384×16384×16384矩阵下，逐张量缩放的量化开销约0.15，而逐行缩放约0.1）。

六、训练与推理的性能考量

（一）训练场景

1.融合缩放内核是关键

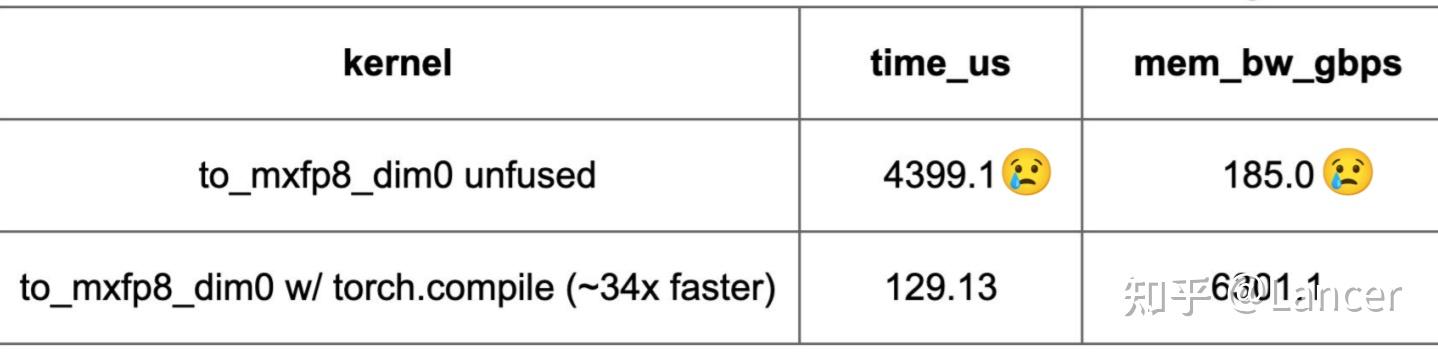
在NVIDIA B200 GPU上，针对16384×16384大小的矩阵（M=K=16384）进行测试，融合的to_mxfp8/to_mxfp4/to_nvfp4内核（将缩放与转换等操作融合）比非融合内核快10倍以上。

2. GEMM矩阵尺寸需足够大

只有当GEMM的矩阵尺寸（MxKxN）足够大时，才能抵消缩放和转换的开销，实现性能加速：

• 性能公式：当bf16的GEMM时间 > 低精度格式（如mxfp8）的GEMM时间 + 低精度格式的缩放开销时间时，低精度格式才具备优势。其中，GEMM时间与矩阵尺寸的三次方成正比（O(M×K×N)），缩放开销时间与矩阵尺寸的平方成正比（O(M×K + M×N + K×N)），因此矩阵尺寸越大，低精度格式的优势越明显。

阈值范围：

• mxfp8：矩阵尺寸需大于约2048×2048×2048（roofline模型上限）。
• mxfp4/nvfp4：矩阵尺寸需大于约1800×1800×1800（roofline模型上限）。

3. 训练流程中需多次量化张量

以mxfp8的矩阵乘法（mm）前向（fwd）和反向（bwd）传播为例：

由于低精度GEMM内核要求第一个操作数为行优先（row-major）、第二个为列优先（col-major），因此输入（input）、权重（weight）、输出梯度（grad_output）需分别按行优先和列优先两种方式量化，共产生6个低精度张量（如mxfp8张量），增加了数据处理的复杂度。

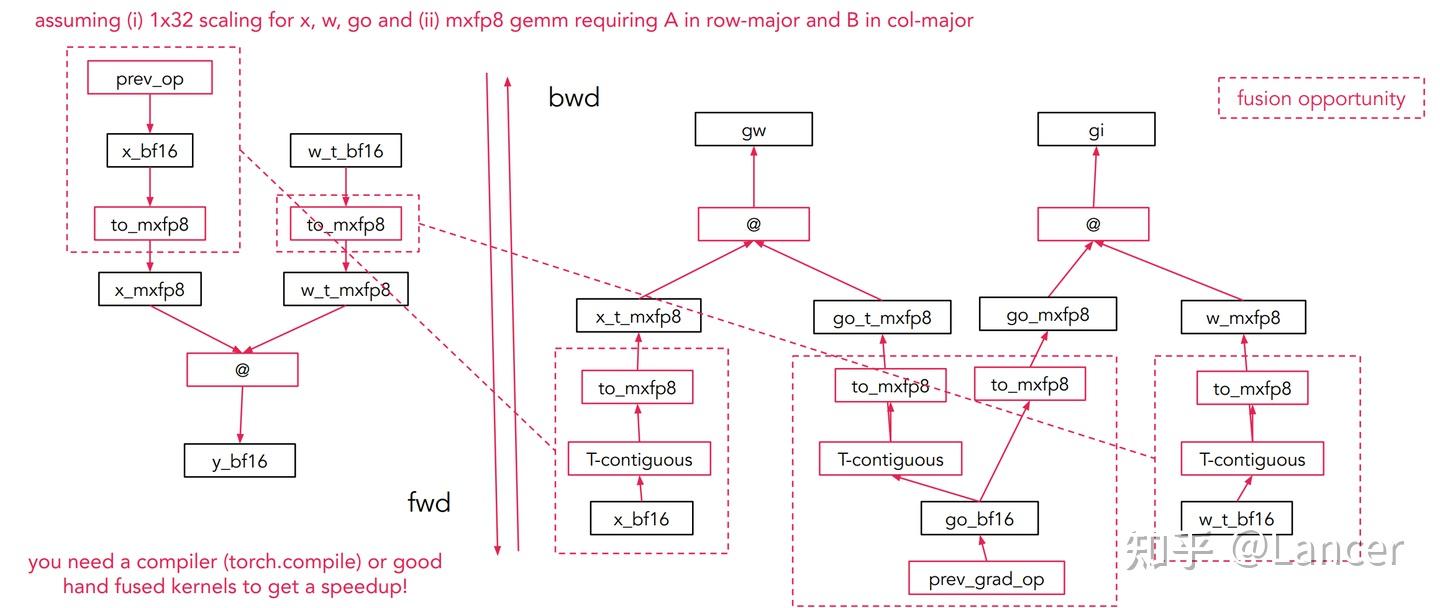
融合需求：需借助编译器（如torch.compile）或手动编写融合内核，将多个操作（如缩放、转换、GEMM）融合，以进一步提升性能。

4. 优化方案：2D 块格式减少权重量化次数

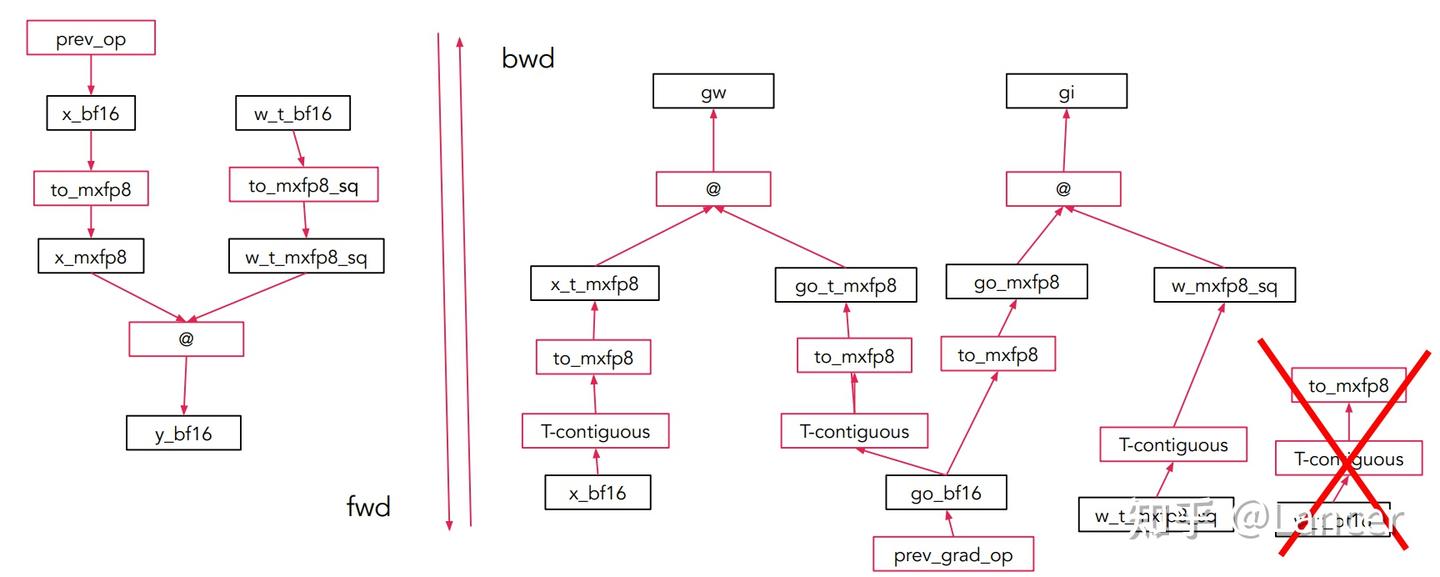
• 将权重矩阵 W 划分为32×32（或 16×16）的二维方块。
• 每个方块整体共享一个 scale（或每行/列共享，但布局对称）。

无论是否转置，这个方块在内存中的 scale 逻辑一致，可实现权重仅量化一次：

（二）推理场景

1. 权重仅需量化一次

推理过程中，权重为固定值，只需在推理前量化一次并存储，推理时直接使用低精度权重；仅需实时量化激活值，减少了量化开销。

2. 融合缩放内核仍为关键

与训练场景一致，融合的to_mxfp8/to_nvfp4内核比非融合内核快10倍以上，可通过torch.compile或手动编写内核实现融合。

3. nvfp4需离线校准全局缩放因子

nvfp4格式需1个全局FP32缩放因子，该因子可在推理前离线校准（基于校准数据集计算），无需实时计算，降低推理时的开销。

4. GEMM矩阵尺寸需足够大

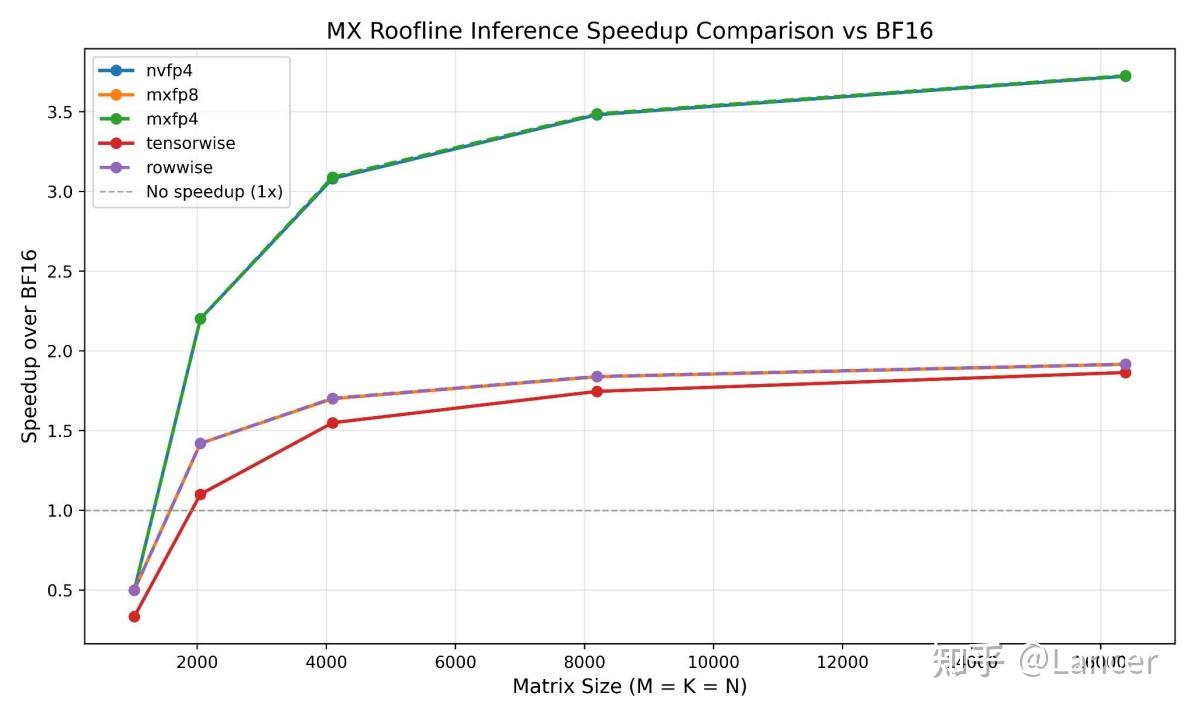
动态激活量化场景下，矩阵尺寸需大于1024×1024×1024或2048×2048×2048，才能抵消量化开销，实现性能加速。从Roofline模型可见，矩阵尺寸越大，mxfp8、mxfp4、nvfp4的加速比越高，nvfp4的最高加速比接近3.5倍，mxfp8接近2倍。

七、总结

参考文献

1.mxfp8, mxfp4, nvfp4 formats and applications in PyTorch，PyTorch Conference 2025
2.Recipes for Pre-training LLMs with MXFP8
3.Pretraining Large Language Models with NVFP4
4.Quartet: Native FP4 Training Can Be Optimal for Large Language Models