本工作于字节跳动完成。首次发布于2025年9月17日。

原文：https://richardli.xyz/rl-collapse

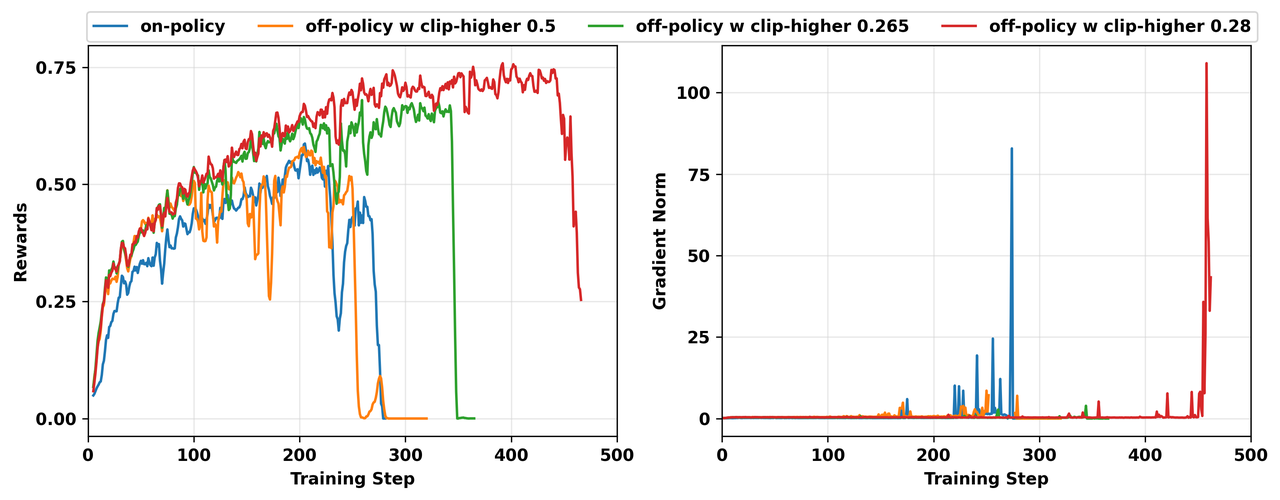
图1. 我们在Qwen3-14B-Base上进行的四次失败的GRPO TIR实验的奖励（左）和gradient norm（右）。所有实验在每个训练步骤采样 1024条轨迹（64个提示词 × 16个回复），学习率为 1e-6。在on-policy和off-policy实验中，ppo_mini_batch_size分别设置为 1024和 256。

要点摘要（TL;DR）：

对更快推理的追求已造成显著的"训练-推理不匹配"，这可能导致大语言模型的RL训练失败。我们的研究揭示了一个正反馈循环问题，在现代reasoning和agent RL中尤为突出：

1、 分布外上下文导致低概率采样： Agent工作流使模型暴露于外部输入和动态环境，导致模型频繁生成低概率token，这些token对于新颖的推理、工具调用和自适应响应至关重要。3.4 分布外工具响应放大不匹配

2、 低概率token加剧训练崩溃： 这些token是训练-推理不匹配最严重的位置，导致异常大的梯度，引发隐性退化和训练失败。3.3 关键发现：低概率Token陷阱

3、 硬件差异使问题复杂化： 不同的GPU架构以不同方式加剧不匹配，这意味着相同的agent训练配置可能在一台机器上成功，而在另一台机器上失败。3.5 环境因素：硬件的关键作用

4、 sequence级别校正是有原理依据的解决方案： sequence级别校正是理论上成立的解决方案。它通过考虑完整的状态轨迹来校正有偏梯度，在不同硬件和复杂任务中恢复训练稳定性。4.2.1 原理性解决方案：分布校正

深入分析：

为了对这个问题进行严谨的理论分析，我们发布了一个新的三部分博客系列以提供深入分析：

[Part 1: 为什么Off-Policy会使得RL优化不稳定 — SGA分析框架]

已知（TRPO理论）： Surrogate目标 L_\mu(\pi) 是RL目标 J(\pi) 的一阶Taylor近似；TRPO下界 J(\pi) \ge L_\mu(\pi) - C \cdot T^2 \cdot D_{TV}^{\max} 表明近似误差随 T^2 增长，要求trust region收缩为 \delta \propto 1/T^2。

我们的洞察： Token级别IS（PPO/GRPO）计算的是 \nabla L_\mu 而非 \nabla J——它校正了token分布但未校正状态分布不匹配（d_\mu \ne d_\pi），导致 O(T^2 \Delta_{\max}) 偏差。

我们通过SGA引理形式化了两种失效模式：偏差（由 D_{TV} 度量）和方差（由 \chi^2-divergence度量）——这两个度量不可互换。

[Part 2: SGA分析框架的应用——Token与Sequence级别校正]

我们的分析： Token级别IS（PPO/GRPO）具有源于surrogate一阶近似误差的 O(T^2 \Delta_{\max}) 偏差；Sequence级别IS无偏但方差呈指数级 O((1+\bar{\chi}^2_{\max})^T)。

我们的解决方案： Seq-TIS通过截断 \rho(y) \to \min(\rho(y), C) 实现可控的偏差-方差权衡。

核心结论： 此偏差是sequence级别问题，当其不可忽略时需要sequence级别的解决方案。

[Part 3: 基于Sequence Masking的Trust Region Optimization]

已知（TRPO理论）： Trust region约束确保surrogate保持为有效近似。

我们的解决方案：
（1）Seq-MIS通过rejection实施Hard Trust Region \mathbb{I}(\rho \le C) \cdot \rho \cdot f，完全排除OOD样本。
（2）Geo-RS使用几何平均 \rho_{\text{geo}}=\rho^{1/T} 实现长度不变的Per-Token Trust Region——这是LLM场景下TRPO hard trust region的实际实现，避免了对长序列的系统性拒绝。

1. 突然崩溃之谜

在大语言模型RL（LLM-RL）快速发展的领域中，突然训练崩溃的现象日益凸显。无论是复杂的reasoning RL还是多轮agent RL，许多人都观察到训练过程在经历一段稳定学习后突然崩溃。

我们最近在对Qwen3模型进行多轮tool-integrated reasoning（TIR）的agent RL实验时遇到了这一问题。这发生在我们L20 GPU集群上GRPO算法的on-policy和off-policy变体中。

图1展示了我们在Qwen3-14B-Base上四次崩溃实验的奖励和梯度范数动态。随着训练的进行，梯度范数突然急剧增大，导致模型崩溃。我们最初的调查集中在常见的原因上：

我们检查了代码，确认我们的agent循环遵循token-in-token-out（TITO）的过程。
我们调整了Adam优化器中的超参数 beta1和 beta2。
我们还对优势进行了批量归一化以平衡更新。
...

然而，这些标准修复方法都无效。由于即使是更简单的on-policy实验也失败了，我们怀疑问题不在于RL算法本身，而在于训练栈的更基础层面。这促使我们调查现代LLM-RL中一个关键且日益普遍的挑战：高度优化的推理引擎与高保真训练框架之间不可避免的差异。

2. 根本性冲突：
推理与训练之间日益扩大的差距

Rollout速度是LLM-RL的核心瓶颈。为了实现所需的大规模吞吐量，现代推理引擎（如vLLM、SGLang、TensorRT-LLM）采用激进的优化策略，如投机解码、低精度计算（INT8/FP8）和专用的批次变体CUDA kernel。在保持采样保真度的同时，现代推理引擎的首要目标是最大化吞吐量，通常以每秒token数来衡量。

相反，训练框架（如FSDP、DeepSpeed、Megatron-LM）必须达到不同的平衡，优先考虑梯度计算的数值稳定性和精度，通常对主权重和优化器状态使用更高精度的格式如FP32。优化优先级和约束上的这种差异造成了不可避免的训练-推理不匹配。 对更快rollout的追求正在使这一差异扩大。

虽然有人可能提议强制执行相同的计算（例如使用"batch-invariant kernel"），但这些解决方案会带来严重的性能损失，与使用高速推理引擎的初衷相悖。这种速度与一致性的权衡是问题的核心，使其成为一个持久的挑战，而非简单的工程修复所能解决。

在我们的技术栈中，这种不匹配具体表现在vLLM推理采样器和FSDP训练器之间。实际的参数更新是：

\mathbb{E} _{x\sim \mathcal{D}}\mathbb{E} _{y\sim \textcolor{red}{\pi _{\theta}^{\mathrm{infer}}}\left( \cdot |x \right)}\left[ R\left( x,y \right) \nabla _{\theta}\log \textcolor{blue}{\pi _{\theta}^{\mathrm{train}}}\left( y|x \right) \right],

而理论上的参数更新应该是：

\mathbb{E} _{x\sim \mathcal{D}}\mathbb{E} _{y\sim \textcolor{blue}{\pi _{\theta}^{\mathrm{train}}}\left( \cdot |x \right)}\left[ R\left( x,y \right) \nabla _{\theta}\log \textcolor{blue}{\pi _{\theta}^{\mathrm{train}}}\left( y|x \right) \right].

其中 x 是从分布 \mathcal{D} 中采样的提示词，y 是回复，R 是奖励函数，\theta 是LLM的参数，\textcolor{red}{\pi^\text{infer}_\theta} 和 \textcolor{blue}{\pi^\text{train}_\theta} 分别是vLLM引擎和FSDP引擎中实现的策略。为了调查这个问题，我们首先需要一种方法来度量它。

3. 训练崩溃剖析

3.0 实验设置

除非另有说明，第3节和第4节中呈现的实验都是在TIR设置下的 VeRL 框架上进行的，使用vLLM v1采样器（AsyncvLLMServer）、Qwen3-14B-Base模型和GRPO算法，全部在L20 GPU集群上运行。

3.1 度量不匹配：`train_infer_kl`指标

度量训练-推理不匹配的一个直接指标是train_infer_kl：

\small{\mathbb{E}_{s\sim d_{\textcolor{red}{\pi^\text{infer}_\theta}}}\left[\text{KL}\left(\textcolor{red}{\pi^\text{infer}_\theta}\left(\cdot|s\right),\textcolor{blue}{\pi^\text{train}_\theta}\left(\cdot|s\right)\right)\right] = \mathbb{E}_{s\sim d_{\textcolor{red}{\pi^\text{infer}_\theta}},a\sim {\textcolor{red}{\pi^\text{infer}_\theta}\left(\cdot|s\right)}} \left[\log\left(\frac{\textcolor{red}{\pi^\text{infer}_\theta}(a|s)}{\textcolor{blue}{\pi^\text{train}_\theta}(a|s)}\right)\right],}

其中 d_\pi 是策略 \pi 的状态占用度量（state occupancy），s 是上下文前缀（状态），a 是token（动作）。注意我们的实验涉及工具调用，这意味着回复 y 可能包含工具响应。因此，我们的 train_infer_kl指标仅考虑模型自身生成的token。

由于我们的实验使用vLLM作为推理引擎，在后续的实验图表中我们将此指标记为 vllm-kl。以下代码提供了在 VeRL 中使用K3估计器计算该指标的实现，假设推理引擎的token概率已经可以获取：

vllm-kl的K3估计器代码块

rollout_log_probs = batch.batch["rollout_log_probs"] # pi_infer
actor_old_log_probs = batch.batch["old_log_probs"] # pi_train
response_mask = batch.batch["response_mask"]
log_ratio = actor_old_log_probs - rollout_log_probs
vllm_k3_kl_matrix = torch.exp(log_ratio) - log_ratio - 1
vllm_k3_kl = masked_mean(vllm_k3_kl_matrix,response_mask)

3.2 警告信号：相关的不稳定性

我们的第一个线索是高 vllm-kl值并非孤立事件，而是与其他不稳定性指标高度相关。

3.2.1 FSDP熵和奖励的波动

在我们的许多实验中，我们观察到 vllm-kl的异常尖峰通常会同时触发FSDP策略 \textcolor{blue}{\pi^\text{train}_\theta} 的熵和奖励的异常波动。图2中的实验结果是一个直观的例子。

从图中可以看出，熵尖峰发生的位置几乎与 vllm-kl尖峰的位置完全对应。虽然在奖励中没有观察到同样显著的相关性，但可以看到在步骤250左右有一个很大的 vllm-kl尖峰，它触发了低质量批次的生成，并导致了该处明显的下降。

这意味着当不匹配较大时，vLLM策略 \textcolor{red}{\pi^\text{infer}_\theta} 和FSDP策略 \textcolor{blue}{\pi^\text{train}_\theta} 都进入了不稳定区域。

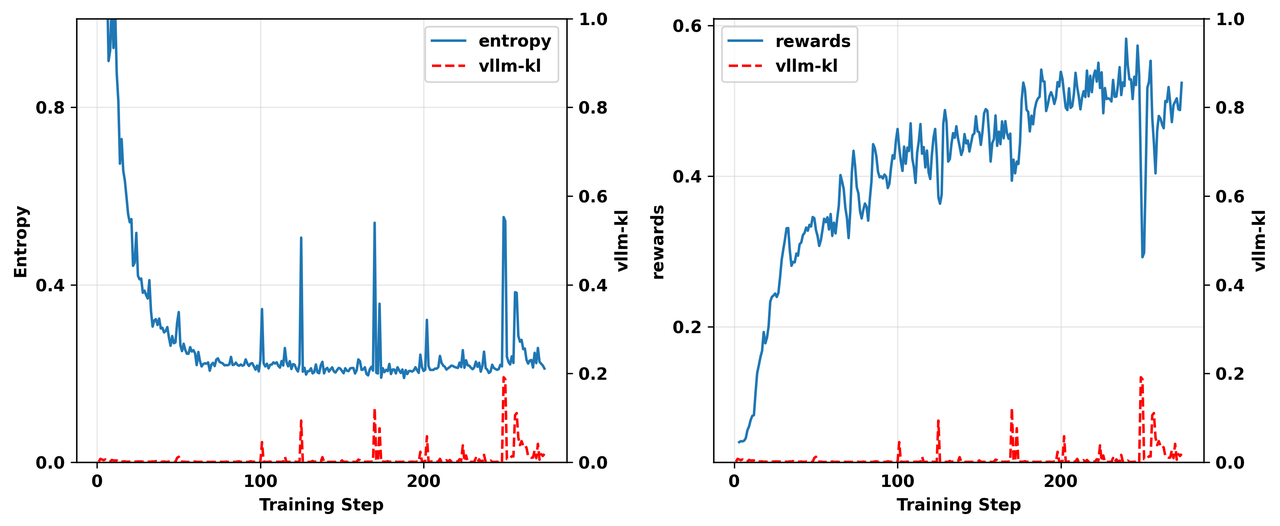
image 1-dvSu.png

图2. 一个on-policy实验结果的对比展示，显示熵（左）和奖励（右）与 vllm-kl 值的对比，说明它们在训练阶段的相关性。

3.2.2 FSDP PPL和gradient norm上升导致策略崩溃

更关键的是，我们观察到 vllm-kl的尖峰同时触发了fsdp-ppl指标和梯度范数（gradient norm）的急剧增大。在我们的实验中，回复 y 的fsdp-ppl指标计算如下：

\text{fsdp-ppl}: \exp\left(\frac{-1}{\left| \mathcal{T} _{\mathcal{M}}\left( y \right) \right|}\sum_{t\in \mathcal{T} _{\mathcal{M}}\left( y \right)}{\log \textcolor{blue}{\pi _{\theta}^{\text{train}}}\left( y_t|y_{<t} \right)}\right)

其中 \mathcal{T} _{\mathcal{M}}\left( y \right) 是回复 y 中模型自身生成的token的索引集。最终的fsdp-ppl指标是批次中所有回复的fsdp-ppl指标的平均值。图3展示了GRPO on-policy版本和off-policy版本的实验结果。

在两个实验中，vllm-kl的尖峰几乎精确地触发了fsdp-ppl和梯度范数的相应急剧增大。此外，可以观察到在训练奖励崩溃之前，vllm-kl指标有显著上升。

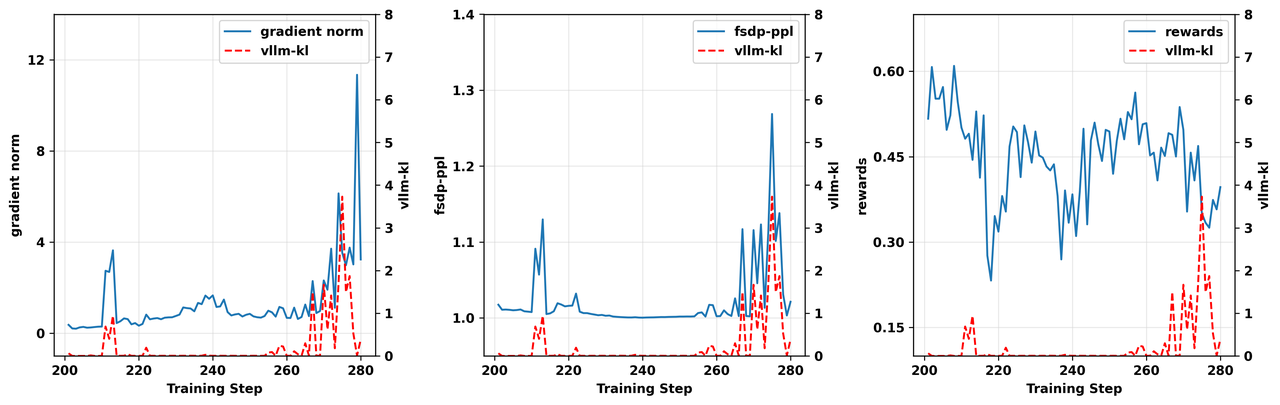
image 2-SOmq.png

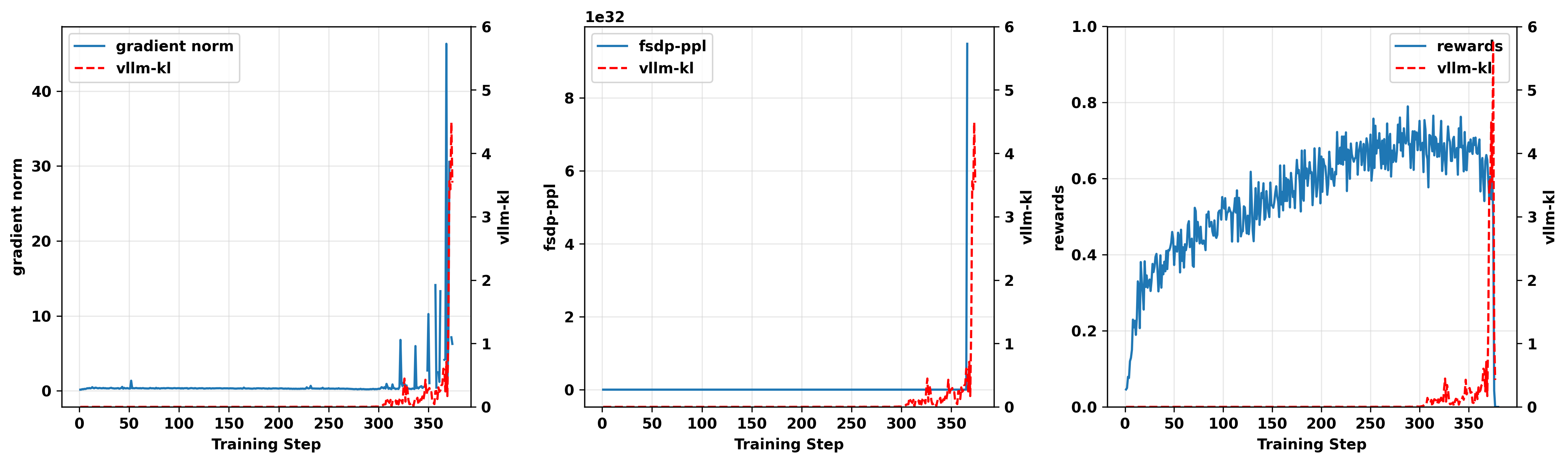
image 3-tKxI.png

图3. 步骤200-280的on-policy实验结果（上）和clip-higher为0.28的off-policy实验结果（下），显示gradient norm*（左）、fsdp-ppl（中）和奖励（右）与 vllm-kl 值的对比，说明它们在训练期间的相关性。*

在我们的实验中，模型自身生成的序列至少包含几百个token。因此，在训练后期阶段，ppl指标保持在1左右更为合理。然而，在训练-推理不匹配显著的批次中——即 vllm-kl显著较高的地方——观察到fsdp-ppl指标急剧增大。

这表明训练引擎为推理引擎策略采样的token分配了极低的概率，从而导致梯度爆炸。 这一观察帮助我们进一步定位了不匹配更可能发生的位置。事实上，正如我们稍后将看到的，当这些在训练引擎中概率极低的token被采样时，它们在推理引擎中的概率并没有那么低。

3.3 关键发现：低概率Token陷阱

不匹配并非均匀分布。

通过分析具有不同 vllm-kl水平的批次，我们发现了一个明显的规律：对于在vLLM推理引擎中概率较低的token，差异最为严重。

当token的推理概率接近零时，训练概率可能变得小几个数量级，导致PPL和梯度趋于无穷大。为确保结论具有足够的普遍性，我们从不同实验的不同训练步骤中选取了训练崩溃前采样的批次。

所有这些批次都表现出相对较高的 vllm-kl值，使我们能够在显著条件下研究不匹配模式。在以下三个 vllm-kl范围内收集了Rollout批次，每组五个批次（约500万token）：

组1（低）： 每个rollout批次的 vllm-kl不超过1e-3，批次使用H20 GPU采样。
组2（中）： 每个rollout批次的 vllm-kl属于[1e-3, 2e-2]，批次使用L20 GPU采样。
组3（高）： 每个rollout批次的 vllm-kl属于[2e-2, 1e-1]，批次使用L20 GPU采样。

下图4(a)(b)(c)展示了vLLM引擎的输出概率，即 \textcolor{red}{\pi^\text{infer}_\theta}(a|s) 与不匹配程度——由 \log\left(\textcolor{blue}{\pi^\text{train}_\theta}(a|s)\right)-\log\left(\textcolor{red}{\pi^\text{infer}_\theta}(a|s)\right) 度量——在不同 vllm-kl量级下的关系：

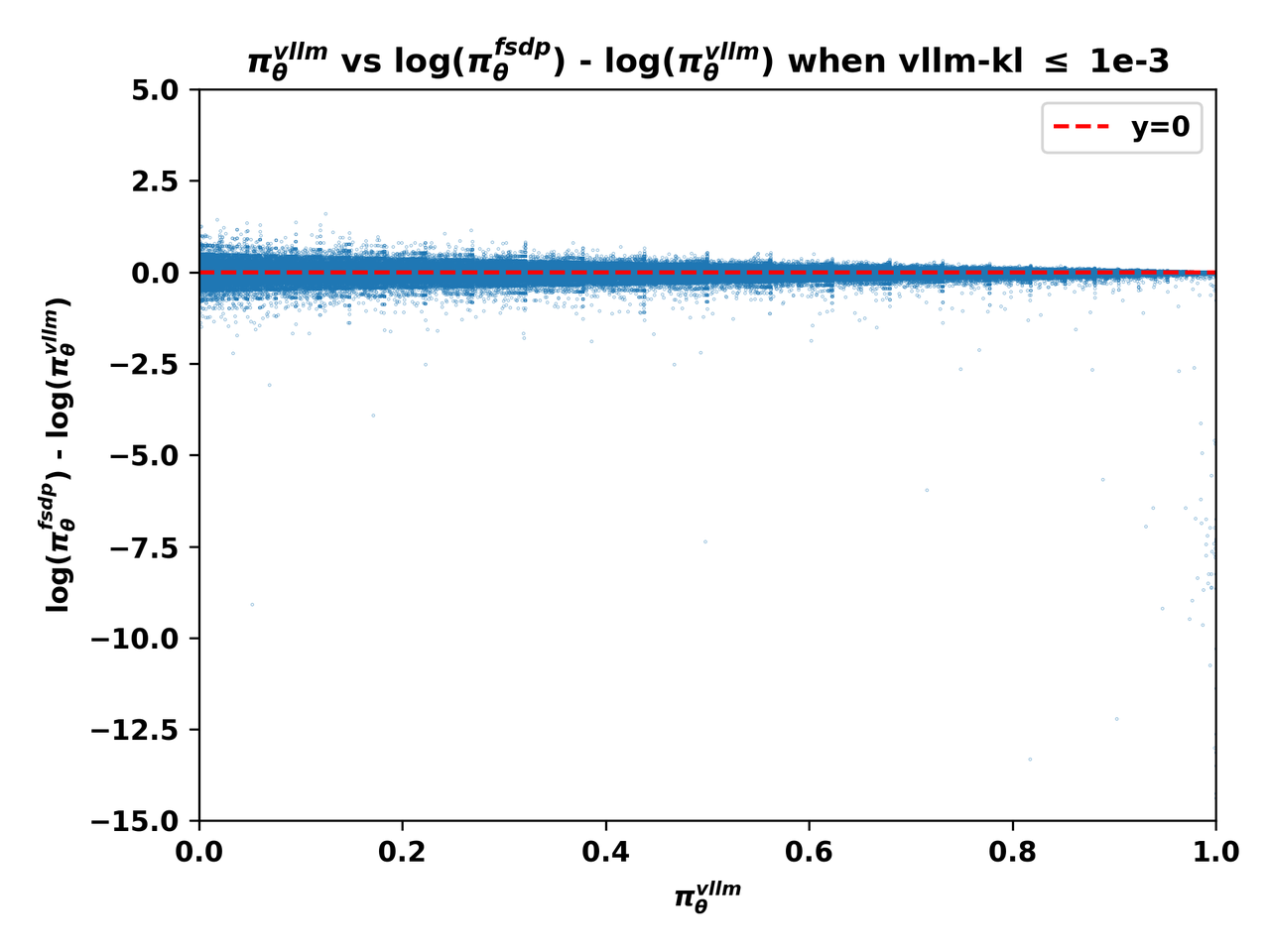
image 4-NMno.png

图4(a). 组1批次中token的 \textcolor{red}{\pi^\text{infer}_\theta} 与 \log\left(\textcolor{blue}{\pi^\text{train}_\theta}\right)-\log\left(\textcolor{red}{\pi^\text{infer}_\theta}\right) 关系图。

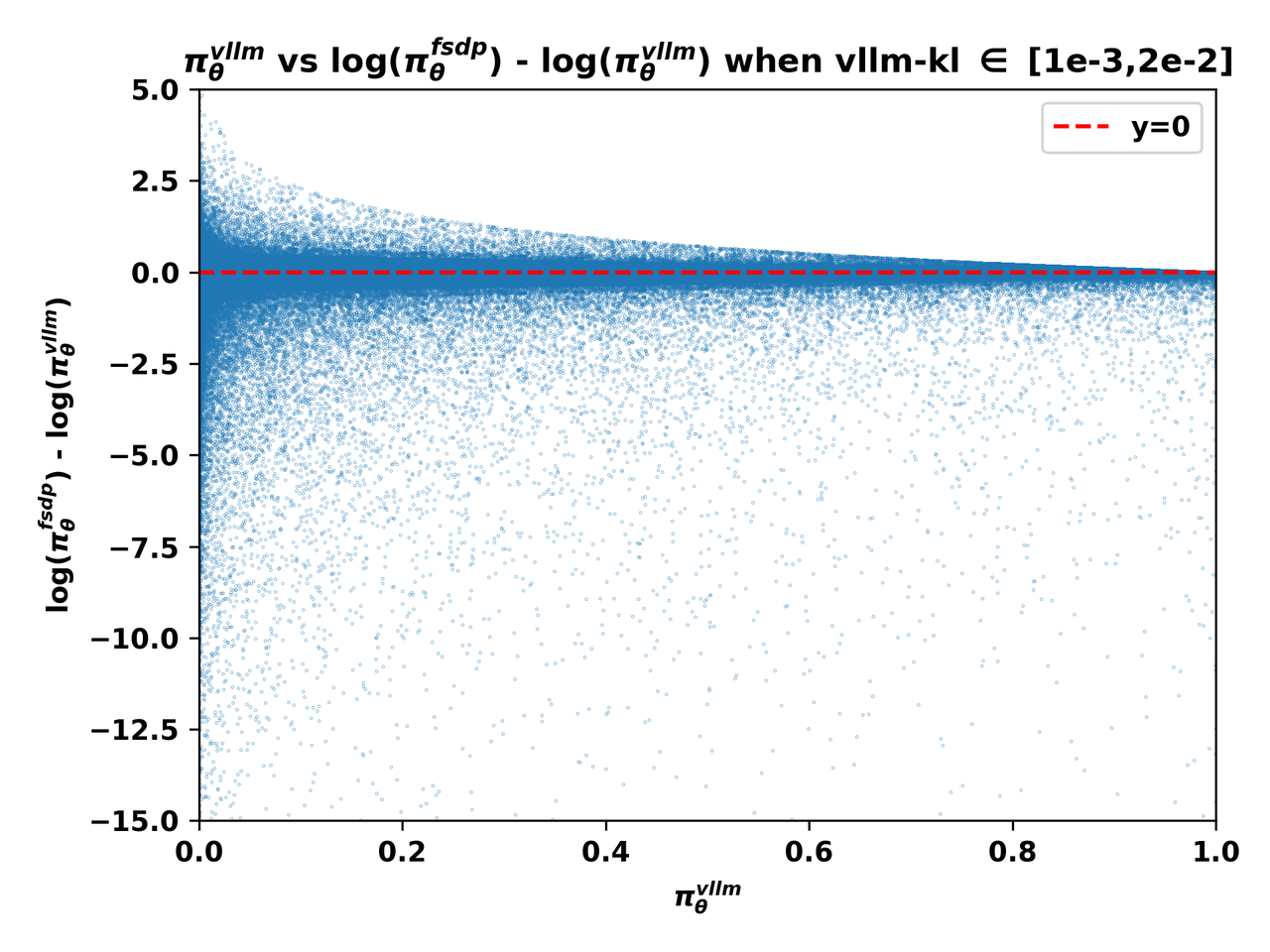
image 5-bqOu.png

图4(b). 组2批次中token的 \textcolor{red}{\pi^\text{infer}_\theta} 与 \log\left(\textcolor{blue}{\pi^\text{train}_\theta}\right)-\log\left(\textcolor{red}{\pi^\text{infer}_\theta}\right) 关系图。

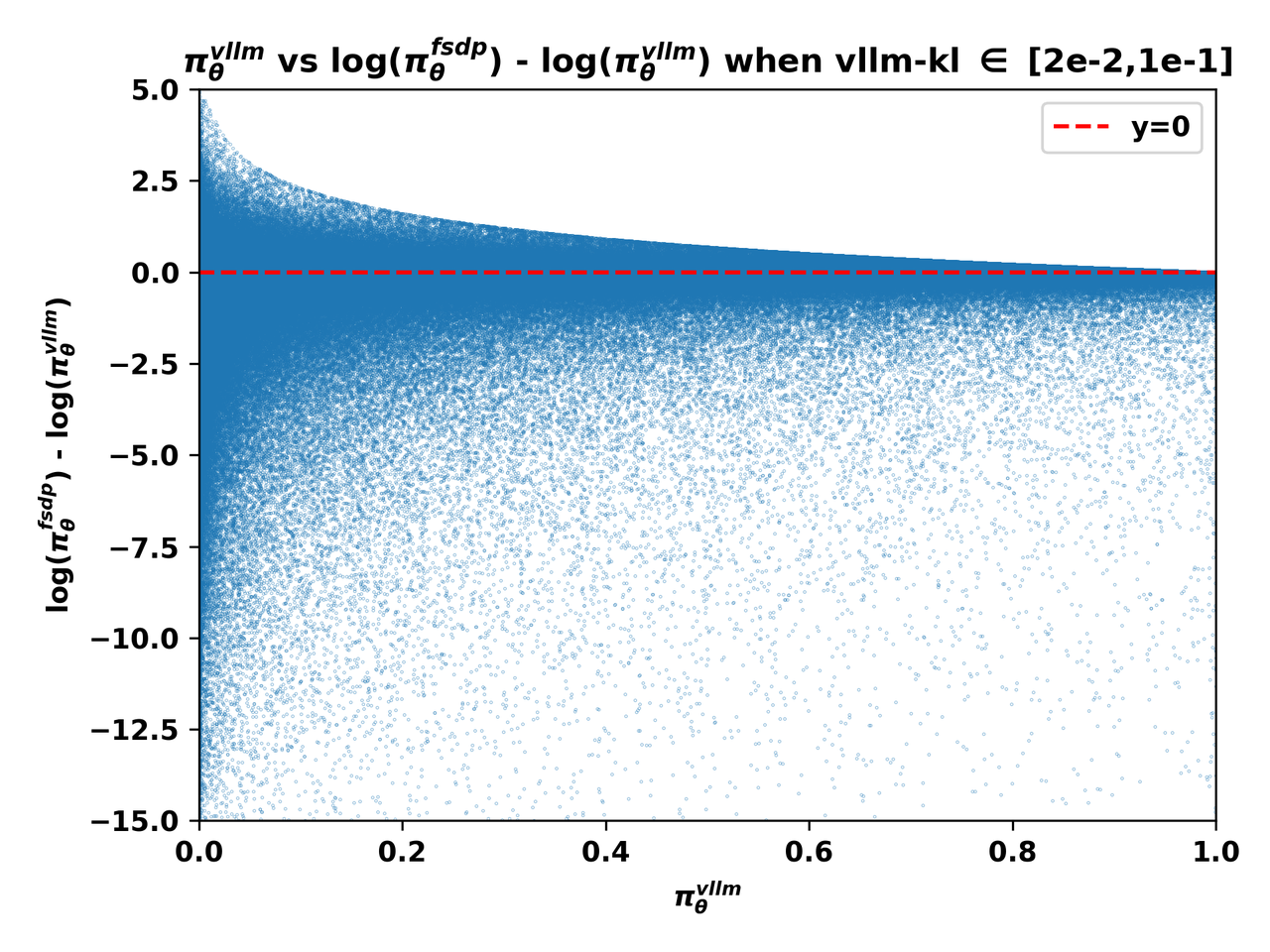
image 6-vZAN.png

图4(c). 组3批次中token的 \textcolor{red}{\pi^\text{infer}_\theta} 与 \log\left(\textcolor{blue}{\pi^\text{train}_\theta}\right)-\log\left(\textcolor{red}{\pi^\text{infer}_\theta}\right) 关系图。

从上述三张图中，我们可以清楚地观察到：

1、当vLLM概率 \textcolor{red}{\pi^\text{infer}_\theta} 接近零时，不匹配程度更加显著，\log\left(\textcolor{blue}{\pi^\text{train}_\theta}\right)-\log\left(\textcolor{red}{\pi^\text{infer}_\theta}\right) 的极端值更可能在这些条件下出现。

2、在L20 GPU上收集的批次，即组2和组3中的批次，其训练-推理不匹配主要表现为FSDP概率 \textcolor{blue}{\pi^\text{train}_\theta} 显著小于vLLM概率 \textcolor{red}{\pi^\text{infer}_\theta}。

3.4 分布外工具响应放大不匹配

3.4.1 非首轮输出中不匹配更严重

第3节的发现解释了为什么这个问题在我们的多轮TIR实验中尤为严重，特别是在非首轮模型输出中。其过程如下：

1、 Agent接收工具响应，这通常是结构化文本（例如被 <python_output>和 </python_output>标签包裹的上下文），相比其预训练和SFT数据属于分布外数据。
2、面对这种不熟悉的分布外上下文，agent的策略变得更加不确定，使其在后续轮次中更容易采样低概率token（这一现象在SimpleTIR中也有观察到）。
3、正如我们刚刚确认的，这些低概率token正是严重不匹配发生的主要位置，为 fsdp-ppl和梯度的急剧增大创造了条件。

接下来，我们绘制三组批次（每组约5k条轨迹）中的不匹配，突出首轮模型输出和非首轮模型输出之间的差异。我们考虑以下两种方法来可视化不匹配：

1、 Log-ppl散点图：x轴表示由vLLM策略 \textcolor{red}{\pi^\text{infer}_\theta} 计算的ppl指标的对数，记为 vllm-log-ppl，y轴表示由FSDP策略 \textcolor{blue}{\pi^\text{train}_\theta} 计算的ppl指标的对数，记为 fsdp-log-ppl。
2、 概率散点图：x轴表示vLLM策略 \textcolor{red}{\pi^\text{infer}_\theta} 的token概率，y轴表示FSDP策略 \textcolor{blue}{\pi^\text{train}_\theta} 的token概率。

我们在下面展示三组的不匹配可视化结果。

组1：vllm-kl ≤ 1e-3的批次

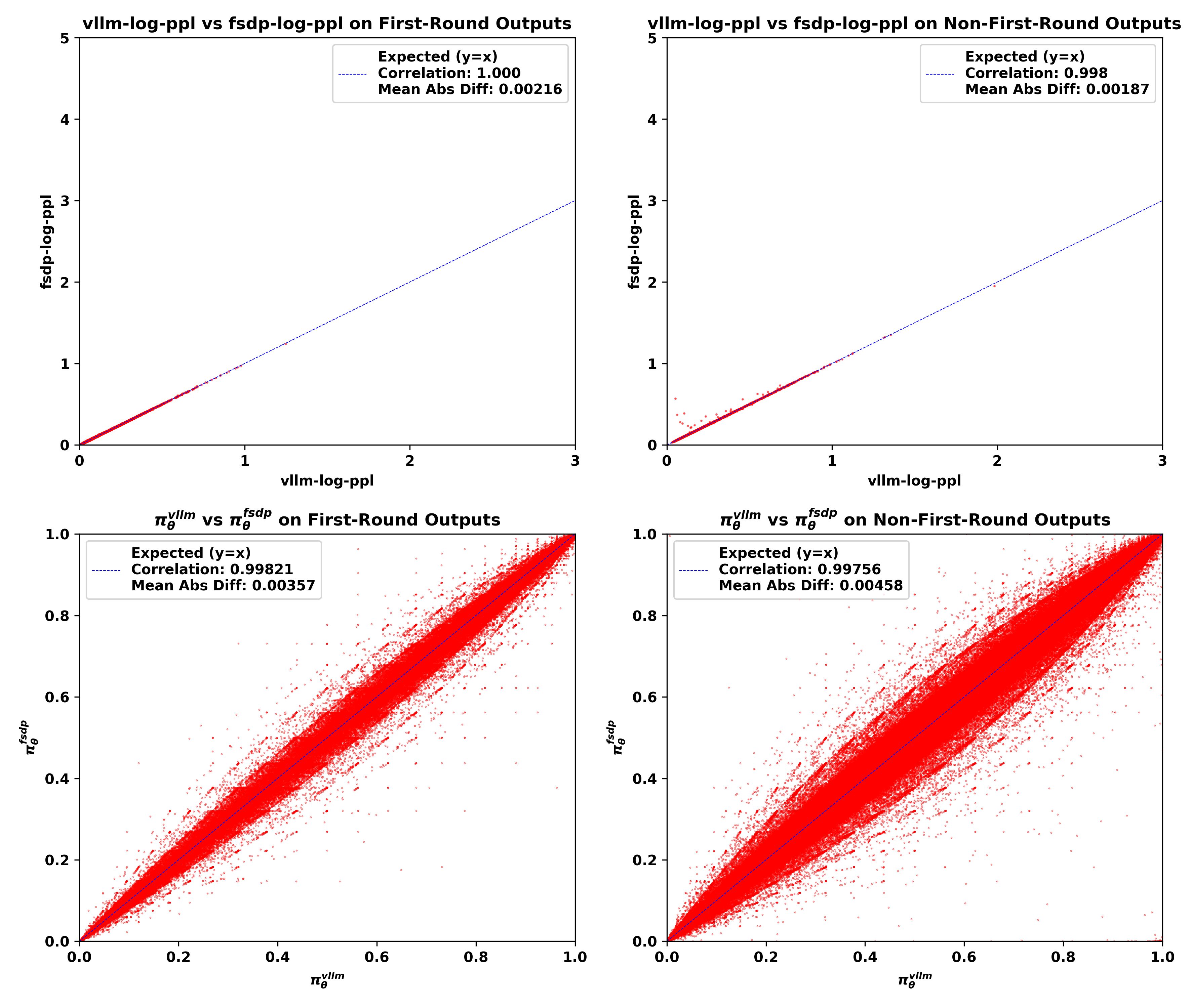
image 7-Bjed.png

组2：vllm-kl ∈ [1e-3, 2e-2]的批次

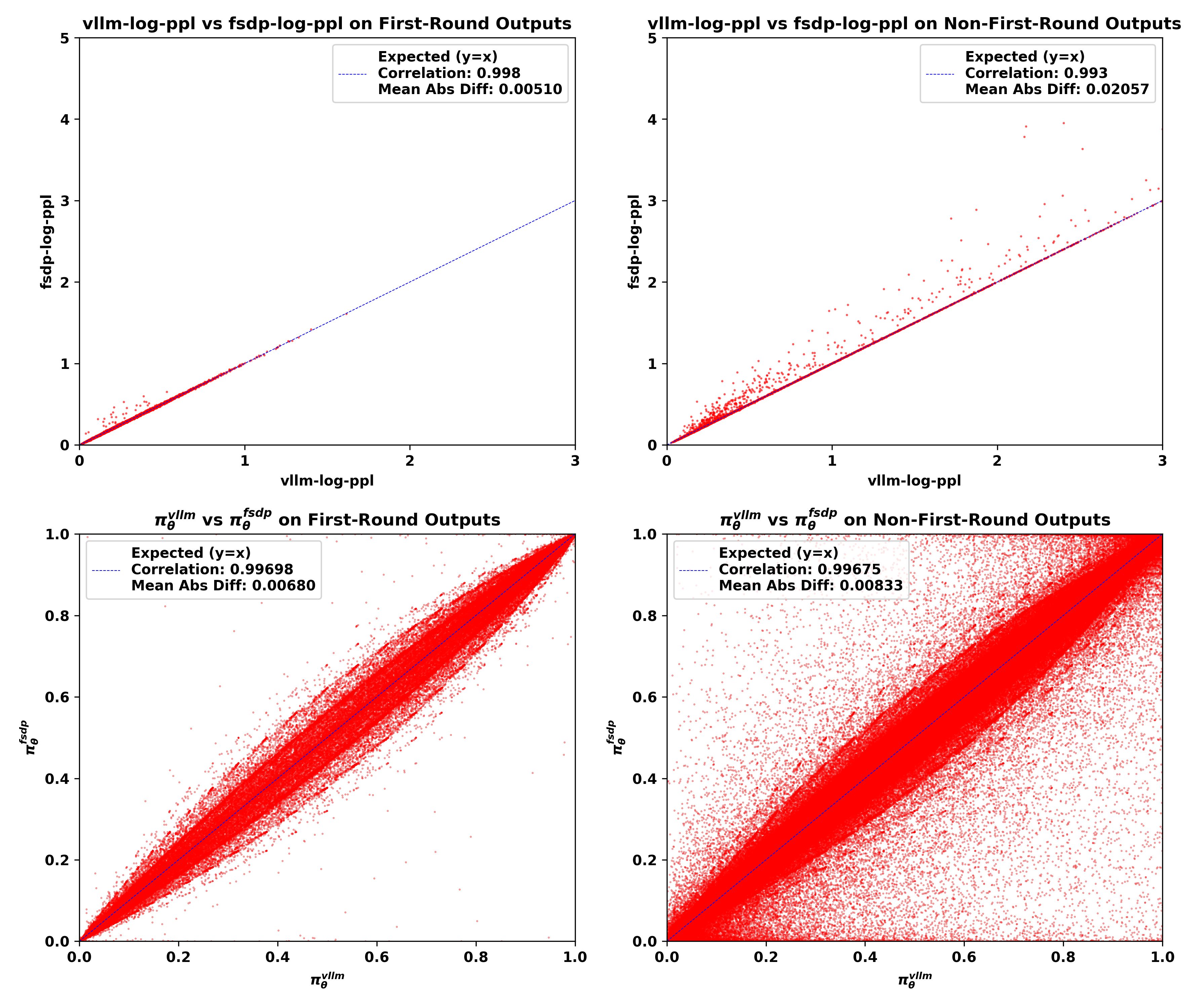
image 8-SZTP.png

组3：vllm-kl ∈ [2e-2, 1e-1]的批次

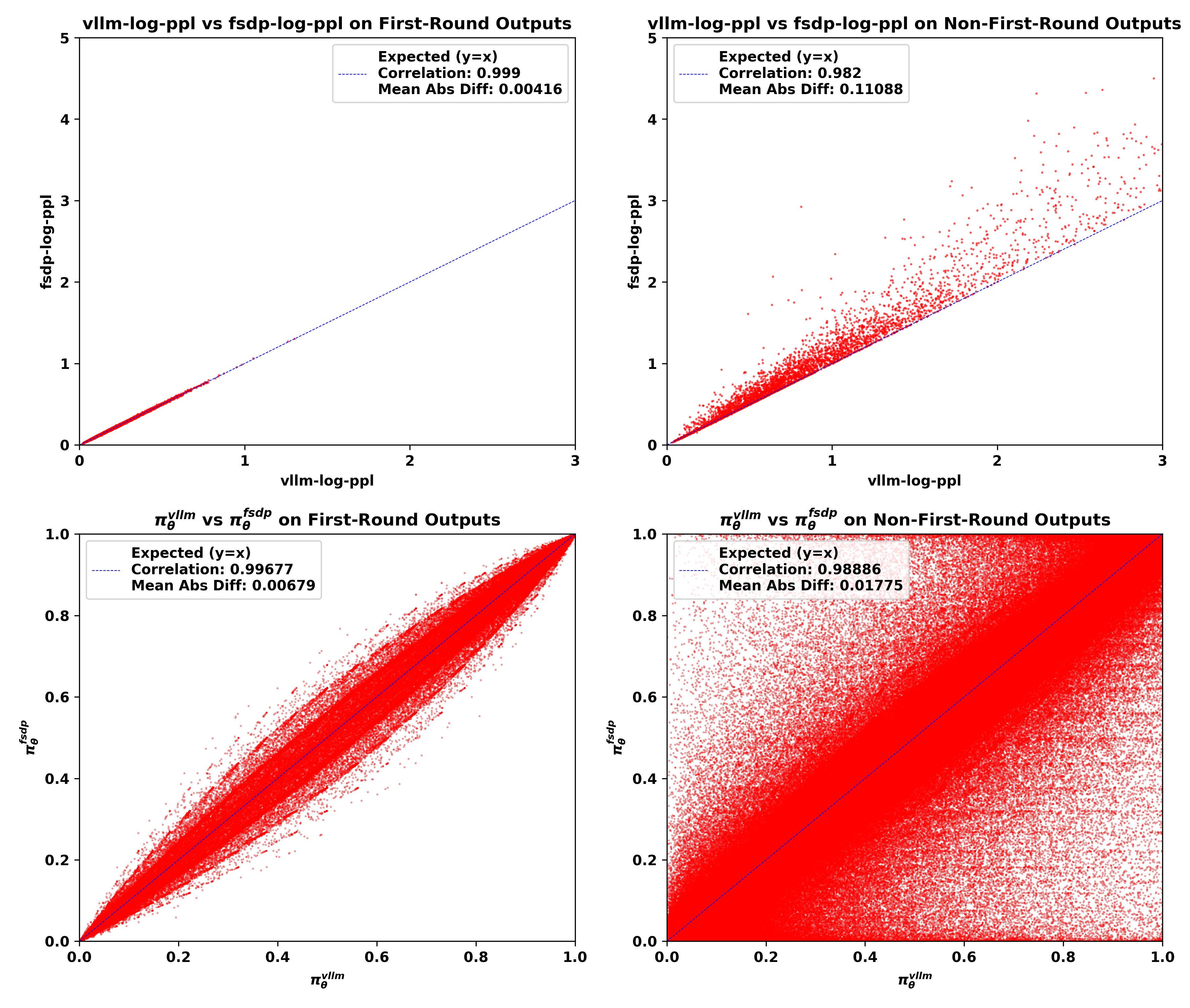
image 9-FOEK.png

从可视化结果中，我们可以观察到：

1、与首轮输出相比，非首轮输出的 vllm-log-ppl通常更大，这意味着面对不熟悉的分布外上下文时，模型采样了更多低概率token。
2、不匹配主要发生在非首轮模型输出中，表现为FSDP策略和vLLM策略之间log-ppl和token概率的平均绝对差异更大，Pearson相关系数更低。
3、随着 vllm-kl值的增加，训练-推理不匹配主要在非首轮输出中恶化。
4、不匹配一致显示 fsdp-log-ppl大于 vllm-log-ppl，表明FSDP引擎产生了更极端的低概率token。

3.4.2 工具调用越多，训练越不稳定

以下实验进一步证明了分布外工具响应会加剧训练-推理不匹配和训练不稳定性。我们在H20 GPU上使用Qwen3-14B-Base作为基础模型进行了off-policy GRPO实验，clip higher=0.28，4个mini-batch。

我们将单条轨迹中工具调用的最大次数（超参数 max_tool_turn）设置为20和100。实验结果如图5和图6所示。可以观察到，随着工具调用次数的增加，训练崩溃发生的时间更早。崩溃时，所有情况下都观察到梯度爆炸和 vllm-kl急剧增大。

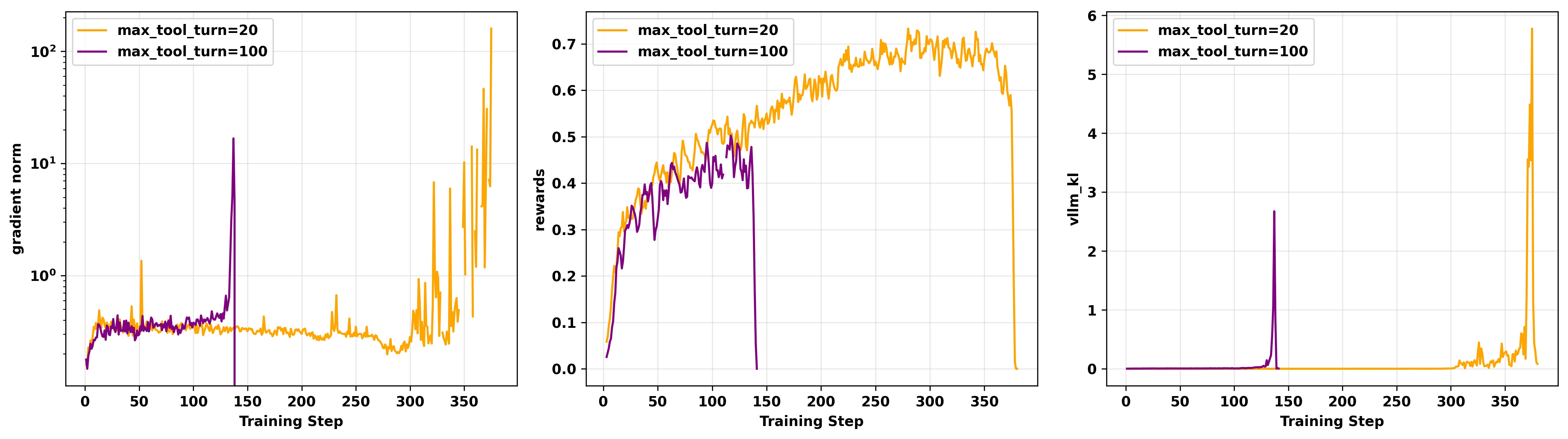
img_v3_02qd_02be3106-7f04-4a29-9e8c-6622066ae05g-ABdf.jpg

图5. 不同 max_tool_turn超参数值的off-policy GRPO实验的gradient norm（左）、奖励（中）和 vllm-kl指标（右）。所有实验都在H20 GPU上进行，使用Qwen3-14B-Base作为基础模型，clip higher=0.28，4个mini-batch。

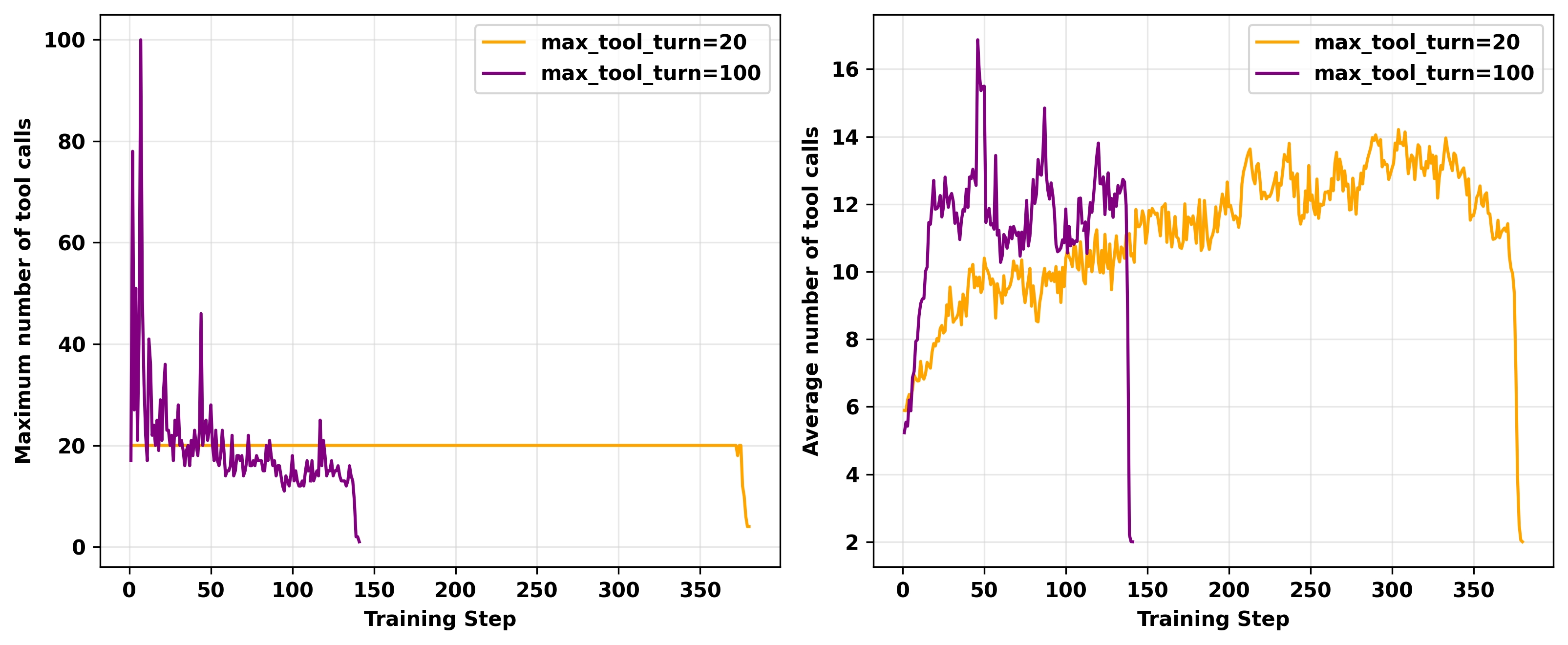
img_v3_02qd_59fb5983-9cf2-4f00-850a-6cfab113c70g-voZF.jpg

图6. 不同 max_tool_turn超参数值的off-policy GRPO实验的工具调用最大次数（左）和平均次数（右）。所有实验都在H20 GPU上进行，使用Qwen3-14B-Base作为基础模型，clip higher=0.28，4个mini-batch。

3.5 环境因素：硬件的关键作用

最后，我们发现物理硬件是一个关键变量。完全相同的代码和模型在不同GPU硬件上产生了显著不同的不匹配程度。为评估不同硬件上的不匹配程度，我们使用相同的代码环境和超参数运行on-policy算法，仅在不同GPU之间切换进行推理和训练。图7展示了在L20、H20和A100上的训练动态。

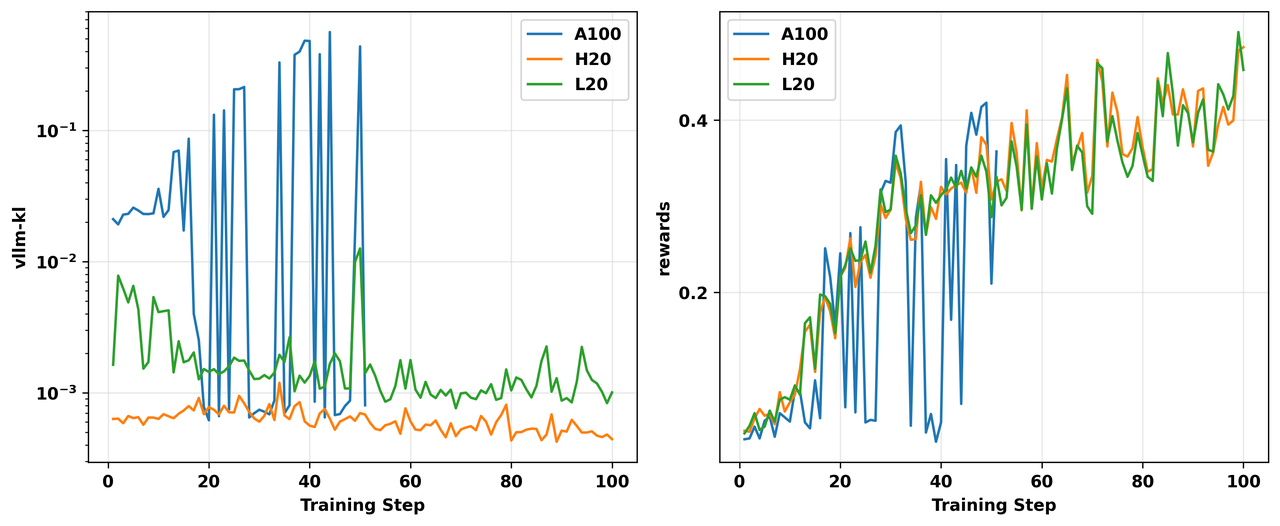
image 10-rszL.png

图7. 不同GPU上GRPO on-policy实验的 vllm-kl指标（左）和奖励（右）。所有实验都在相同的代码和环境上进行。

从图中可以观察到，在我们的实验中，vllm-kl的量级基本遵循：H20 < L20 < A100。具体来说，H20的 vllm-kl通常在5e-4到1e-3的数量级，L20约为1e-3到1e-2，而A100主要在1e-2到1之间。由于A100上严重的训练-推理不匹配，正常训练变得不可行，导致高度不稳定的奖励曲线。

我们发现在vLLM引擎中禁用级联注意力对于减少在A100 GPU上运行的实验中的不匹配特别有帮助。根本原因是FlashAttention-2 kernel中一个不易察觉的bug：

在A100（以及L20）上，特定的batch/sequence长度组合会触发kernel的 split_kv路径，该路径错误地转置了LSE（log-sum-exp）布局，导致Cascade Attention出现完全的精度崩溃，这正是我们观测到的巨大 vllm-kl的来源。

我们在4.2.4 在vLLM中禁用级联注意力中展示这些结果。

最直接的验证来自于当我们将一个失败的L20实验从检查点在H20 GPU上恢复时（见图8）。训练立即稳定并恢复，表明硬件对该问题具有关键影响。

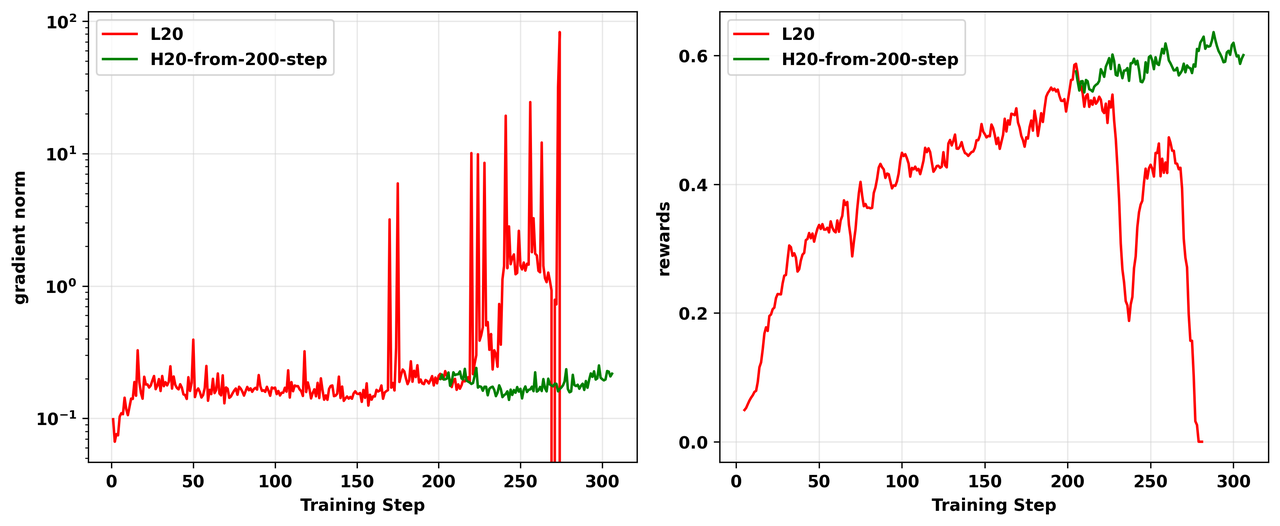
image 11-YkFU.png

图8: L20和H20之间on-policy GRPO实验的对比结果，显示gradient norm（左）和奖励（右）。我们从失败的L20实验（红线）第200个训练步骤的检查点开始在H20 GPU上开始实验（绿线）

3.6 不匹配不是静态的：优化驱动的反馈循环

有人可能认为训练-推理不匹配是硬件和软件栈的静态属性。然而，我们下面的"批次过滤"实验表明不匹配与训练动态和模型状态是相互关联的。

我们在"批次过滤"实验中设置了以下策略更新策略：对于每个训练步骤，如果收集的批次产生的 vllm-kl指标大于阈值，我们跳过在该批次上更新模型参数，因为这样的更新容易导致训练崩溃。

相反，我们直接进入下一步，继续数据收集，直到获得 vllm-kl值低于阈值的批次，此时模型才被更新。

这个实验背后的逻辑是：如果不匹配程度完全独立于模型的输出分布和训练动态，那么 vllm-kl的量级在不同训练步骤之间应该表现出相同的分布。

然而，图9中的实验结果表明，一旦模型进入某种状态，它就会开始持续生成高不匹配批次，从而导致训练停滞。这一现象，以及在其他运行中观察到的 vllm-kl和 fsdp-ppl持续上升的模式（图10），指向一个反馈循环。

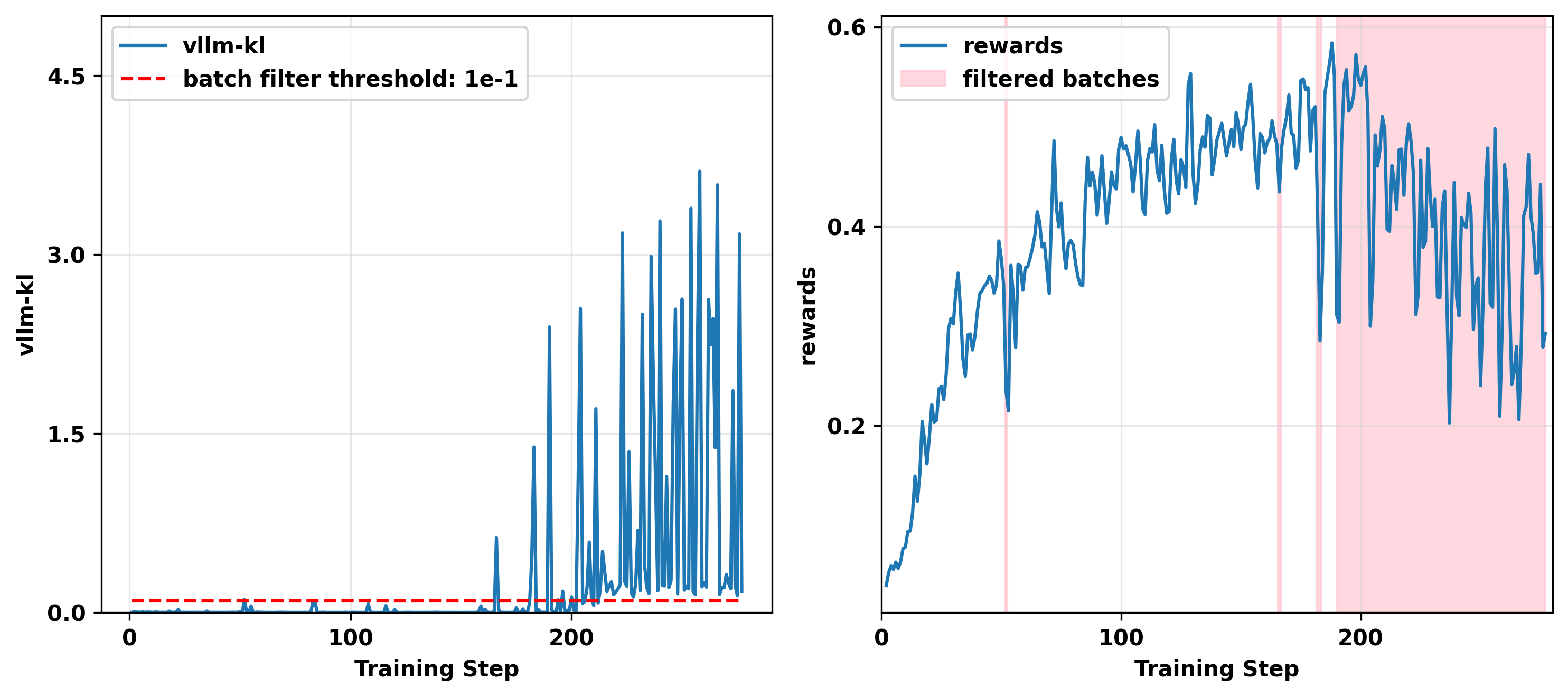
image 12-hGVE.png

图9. 我们on-policy"批次过滤"实验的结果，显示 vllm-kl （左）和奖励*（右），被过滤掉批次的训练步骤用粉色标出。过滤阈值设置为0.1。*

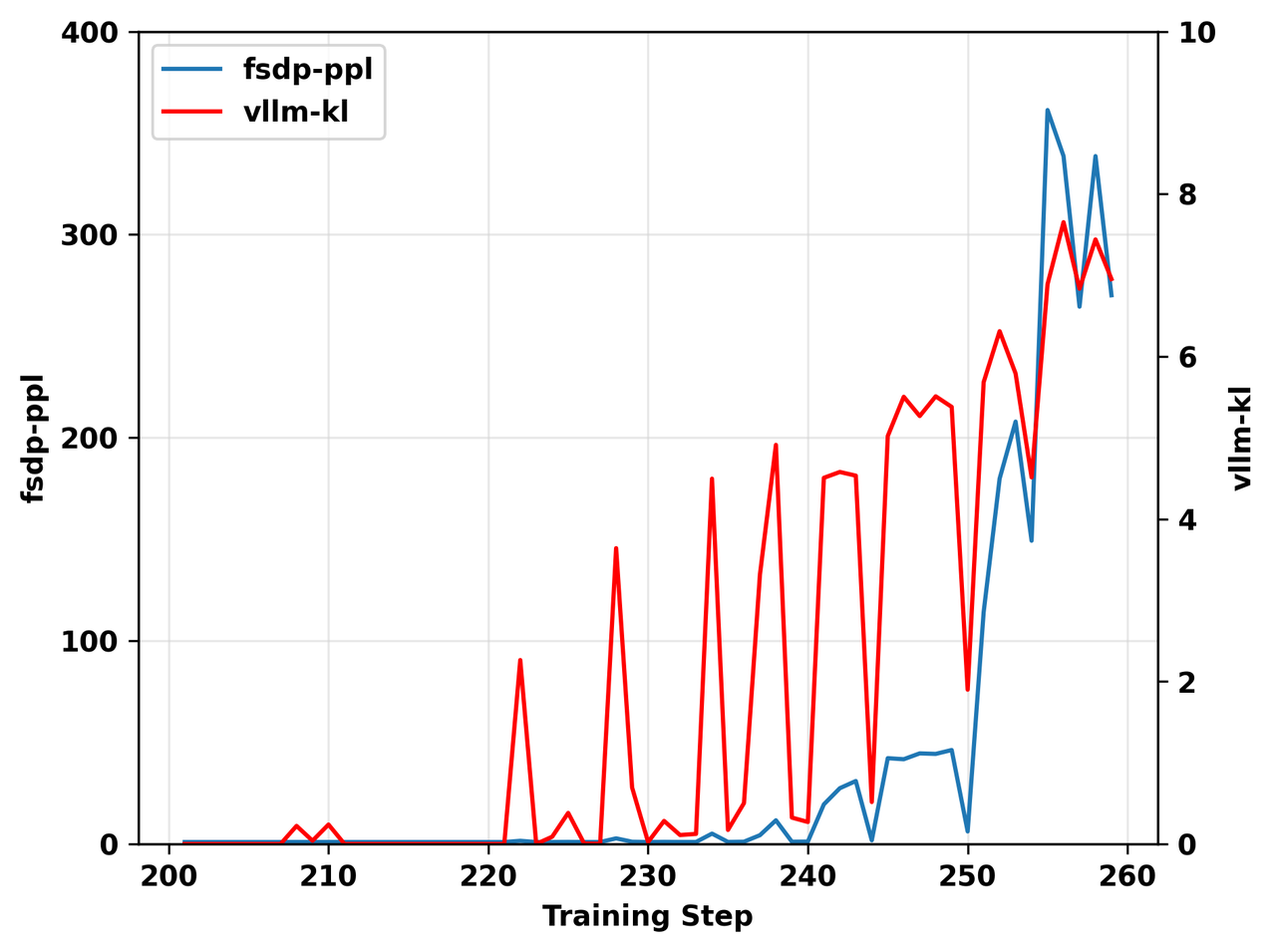
image 13-Woce.png

图10. 一个on-policy实验的结果，描绘了训练步骤上的 vllm-kl 和fsdp-ppl。两条线表现出相关的持续上升模式。

我们假设这是由于以下两阶段级联失效：

1、 阶段1：数值敏感性增加。 RL优化器将模型的权重推入 bfloat16数据类型相对精度较低的数值范围（例如非常小或非常大的值）。
2、 阶段2：Kernel驱动的误差放大。 这些初始的、微小的 bfloat16量化误差随后被输入到vLLM和FSDP的不同kernel中。不同的计算顺序会产生非线性放大效应，导致小的初始偏差在最终logits中累积放大为大的差异。

这形成了一个反馈循环：不匹配导致有偏差且噪声较大的梯度，可能将参数进一步推入数值敏感区域，进而使下一次迭代的不匹配进一步恶化，直到系统崩溃。

4. 缓解训练-推理不匹配的尝试

接下来，我们将列出尝试过的缓解训练-推理不匹配的方法。其中一些方法有所帮助，而另一些则无效。

4.1 无效尝试

4.1.1 使用FP32 LM Head

受到Minimax-M1技术报告和博客文章《你的高效RL框架悄悄地给你带来off-policy RL训练》的启发，我们修改vLLM将lm_head转换为fp32精度。

然而，在我们的实验中，修改后不匹配问题仍然存在，模型崩溃不可避免。图11展示了在L20 GPU上使用vLLM引擎中bf16 lm_head的失败的on-policy实验，以及从崩溃实验的第200个训练步骤开始在vLLM引擎上使用fp32 lm_head的实验。

可以观察到两个实验最终都崩溃了，使用fp32 lm_head的实验仍然表现出 vllm-kl急剧增大。

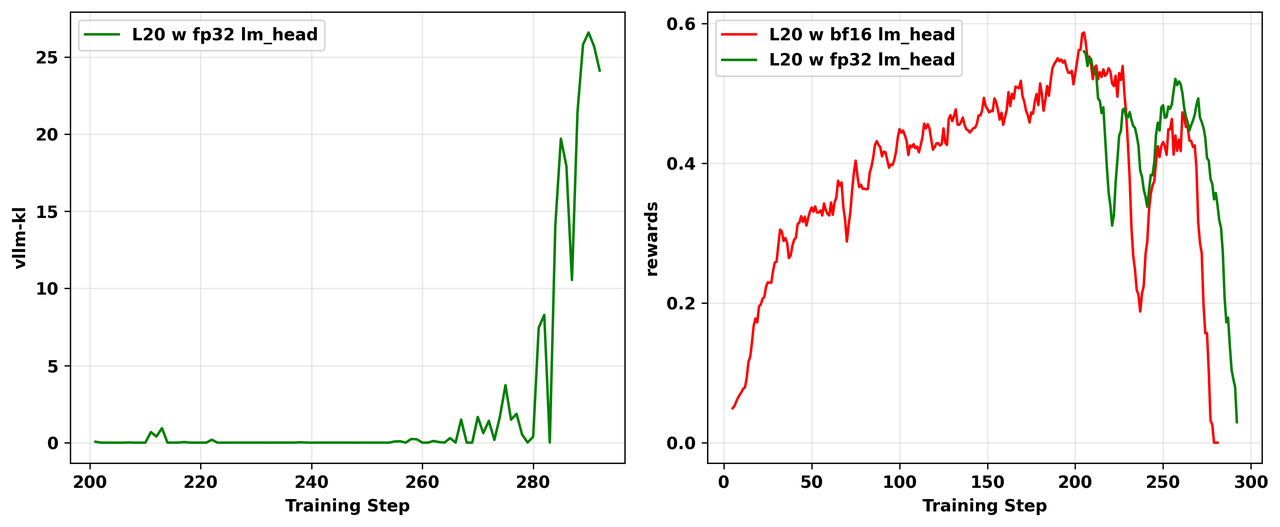
image 14-MPID.png

图11: vLLM引擎中lm_head精度的消融研究结果。左：vllm-kl指标的动态。右：训练奖励的动态。我们从使用bf16 lm_head的失败实验的第200个训练步骤开始，用fp32 lm_head*恢复RL训练。*

4.1.2 禁用分块预填充

我们还尝试从4.1.1节中使用bf16 lm_head的失败实验的第200个训练步骤恢复RL训练，禁用分块预填充以查看是否可以解决崩溃。然而，我们的实验结果（如图12所示）表明这种方法没有解决崩溃问题。

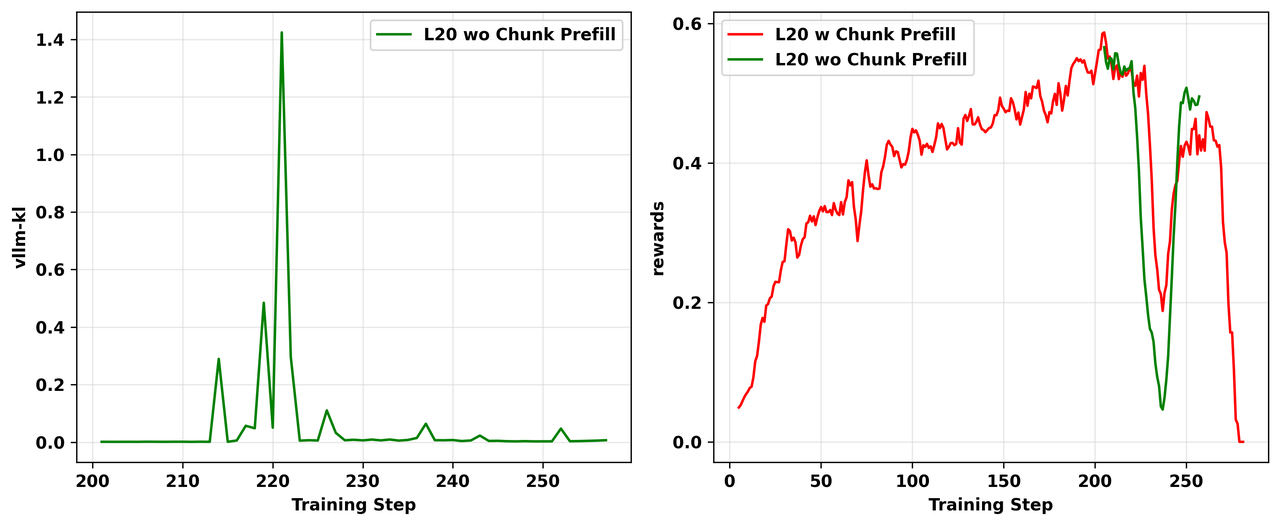
image 15-nLYb.png

图12: 使用分块预填充的消融研究结果。我们从之前启用分块预填充进行的失败实验的第200个训练步骤开始，禁用分块预填充重新运行RL训练。左：vllm-kl指标的动态。右：训练奖励的动态。

4.1.3 启用 `enforce_eager`和 `free_cache_engine`

VeRL的DAPO官方配方提到启用CUDA图（enforce_eager=False）可能导致模型性能下降。为了调查它是否影响训练-推理不匹配，我们进行了消融研究以检查vLLM引擎超参数 enforce_eager与另一个超参数 free_cache_engine的影响。

我们在reasoning RL上进行了实验。我们在H100 GPU上使用Qwen3-4B-Base作为基础模型进行on-policy GRPO实验，共运行四种实验设置：超参数 enforce_eager和 free_cache_engine的穷举组合，每个设置为 True或 False。性能在AIME24基准上评估。实验结果如图13所示。

从图中可以看出，调整 enforce_eager和 free_cache_engine的值对训练-推理不匹配和测试性能没有显著影响。

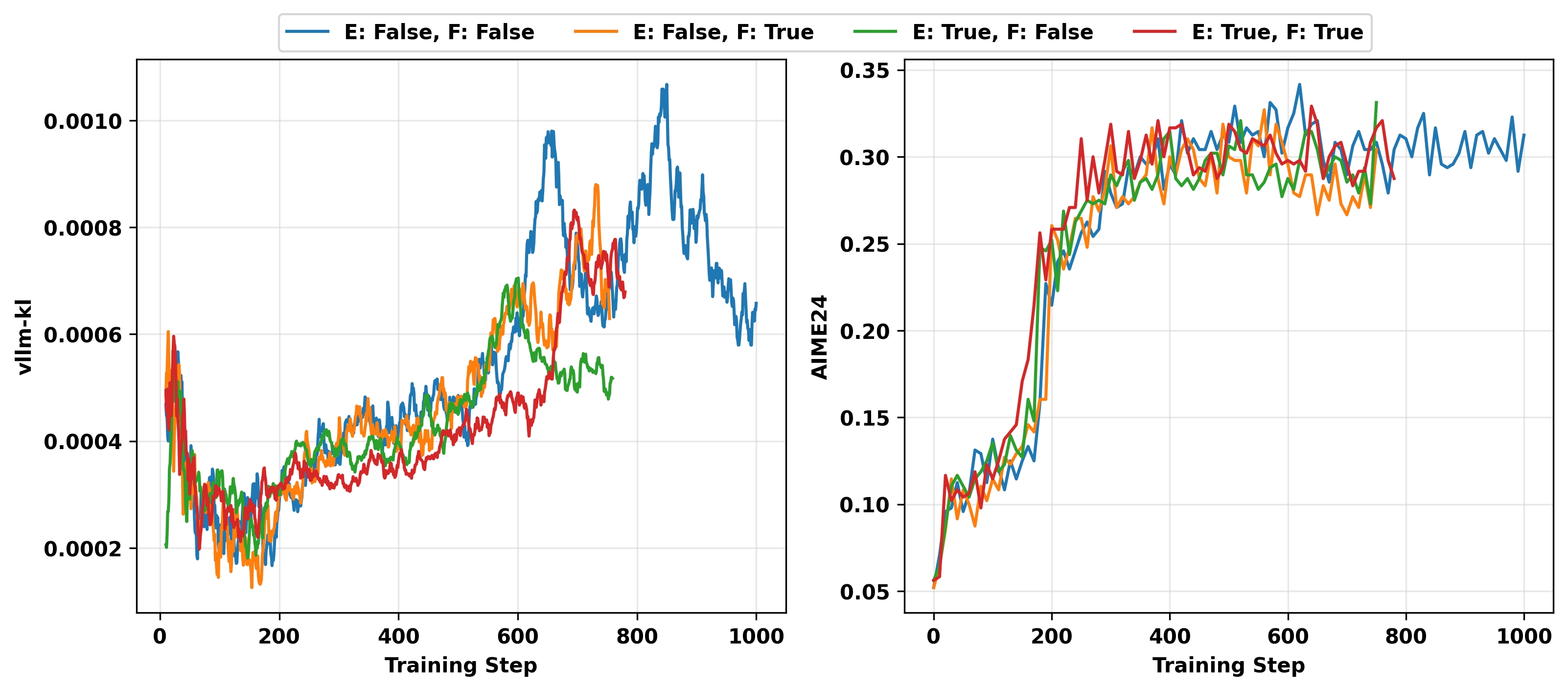
img_v3_02q6_6448e044-312b-4d6e-9761-d8a86c27c91g-XovQ.jpg

图13: reasoning RL中 vLLM 加速和缓存相关超参数的消融研究。我们在H100 GPU上用超参数 enforce_eager（E）和 free_cache_engine（F）的四种可能组合进行on-policy GRPO实验。左：vllm-kl指标的动态。右：AIME24准确率的动态。

4.2 有效尝试

4.2.1 原理性解决方案：分布校正

训练-推理不匹配将我们原本的on-policy RL问题变成了off-policy问题，其中用于生成rollout的策略（behavior policy，\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}）与正在训练的策略（target policy，\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}）不同。校正这种分布偏移的一个理论上可行的方法是重要性采样（importance sampling，IS）。然而，重要性采样的具体形式对于保持无偏梯度和实现稳定训练至关重要。

受(Yao et al., 2025)的发现启发——该工作首次强调了由于训练-推理不匹配而导致的这种隐式off-policy问题——我们分析了两种主要的重要性采样形式：理论上可行的sequence级别IS和常见但有偏的token级别IS近似。

有原理依据的估计器：sequence级别IS

正确的、无偏的策略梯度估计器对整个生成的序列（轨迹）y 应用单一的重要性比率。这正确地将期望从behavior policy重新加权到target policy，产生目标函数 J(\theta) 的真实梯度。

让我们逐步推导sequence级别IS估计器 g_{\mathrm{seq}}(\theta)。

1、目标是最大化目标FSDP策略下的期望奖励：

J(\theta) = \mathbb{E}_{x \sim \mathcal{D}, y \sim \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(\cdot|x)}[R(x,y)]

2、因此真实的策略梯度是：

g(\theta) = \nabla_{\theta} J(\theta) = \mathbb{E}_{x \sim \mathcal{D}, y \sim \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(\cdot|x)}\left[R(x,y) \nabla_{\theta} \log \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(y|x)\right]

3、由于我们只能从vLLM策略进行采样，我们使用重要性采样来转换期望的分布：

g_{\mathrm{seq}}(\theta) = \mathbb{E}_{x \sim \mathcal{D}, y \sim \textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}(\cdot|x)}\left[ \frac{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(y|x)}{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}(y|x)} \cdot R(x,y) \cdot \nabla_{\theta} \log \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(y|x) \right]

这本质上是off-policy REINFORCE算法（Williams, 1992）。这个估计器在数学上等价于策略梯度的标准优势形式。关键在于证明重要性采样比率能精确校正期望，揭示出隐藏在下面的真实on-policy梯度，然后可以进一步细化。最终的优势形式为：

g_{\mathrm{seq}}(\theta) = \mathbb{E}_{s \sim d_{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}}} \mathbb{E}_{a \sim \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(\cdot|s)} \left[ A^{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}}(s,a) \cdot \nabla_{\theta} \log \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(a|s) \right]

其中，s=(x,y_{<t}) 是状态（前缀），a=y_t 是动作（token）。项 d_{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}} 是目标FSDP策略下的状态占用度量（state occupancy）。它被正式定义为遵循策略 \pi 时访问状态 s 的期望次数：

\textcolor{blue}{d_{\pi}(s) := \mathbb{E}_{x' \sim \mathcal{D}, y' \sim \pi(\cdot|x')} \left[ \sum_{t'=0}^{|y'|-1} \mathbb{I}\{ (x', y'_{<t'}) = s \} \right] = P(x) \cdot \prod_{k=0}^{t-1} \pi(y_k|x,y_{<k})}

这个估计器是无偏的，意味着 g_{\mathrm{seq}}(\theta) = g(\theta)。为了数值稳定性，使用截断重要性采样（Truncated Importance Sampling，TIS），它将sequence级别比率 \rho(y|x) 裁剪在常数 C。

一个常见的有偏估计器：Token级别IS

一种常见的启发式方法，通常受PPO等算法启发并在(Yao et al., 2025)中使用，采用逐token的重要性比率。虽然这通常比sequence级别比率具有更低的方差，但它是一个对自回归模型理论上不成立的有偏估计器。

让我们推导Token级别IS梯度估计器，g_{\mathrm{tok}}(\theta)。

1、该公式首先在时间步求和内部错误地应用重要性采样比率：即 g_{\mathrm{tok}}(\theta) 定义为

\mathbb{E}_{x \sim \mathcal{D}, y \sim \textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}(\cdot|x)}\left[ R(x,y) \cdot \sum_{t=0}^{|y|-1} \frac{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(y_t|x,y_{<t})}{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}(y_t|x,y_{<t})} \cdot \nabla_{\theta} \log \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(y_t|x,y_{<t}) \right]

2、我们可以将这个轨迹上的期望重写为vLLM策略下访问的状态上的期望：

g_{\mathrm{tok}}(\theta) = \mathbb{E}_{s \sim d_{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}} \mathbb{E}_{a \sim \textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}(\cdot|s)} \left[ \frac{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(a|s)}{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}(a|s)} \cdot A^{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}(s,a) \cdot \nabla_{\theta} \log \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(a|s) \right]

3、 注意：这里， R(x,y) 是由 \textcolor{red}{\pi_{\theta}^{\mathrm{infer}}} 采样的完整轨迹的经验回报，它作为状态-动作价值 Q^{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}(s,a) 的Monte Carlo估计。 引入基线并改变动作上的期望给出最终形式：

g_{\mathrm{tok}}(\theta) = \mathbb{E}_{s \sim d_{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}} \mathbb{E}_{a \sim \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(\cdot|s)} \left[ A^{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}(s,a) \cdot \nabla_{\theta} \log \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}(a|s) \right]

这个最终表达式清楚地揭示了token级别IS的梯度偏差。可以清楚地观察到，J(\theta) 能够被 g_\text{tok}(\theta) 优化当且仅当 \textcolor{red}{\pi_{\theta}^{\mathrm{infer}}} 保持在 \textcolor{blue}{\pi_{\theta}^{\mathrm{train}}} 的置信域（trust region）内，此时 d_{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}\approx d_{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}} 且 A^{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}\approx A^{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}}。

Token级别IS中的偏差来源

将 g_{\mathrm{tok}}(\theta) 与真实梯度 g_{\mathrm{seq}}(\theta) 进行比较，揭示了两个独立且重要的错误，使token级别估计器有偏。

来源1：状态占用不匹配

合理的off-policy校正必须考虑两个分布偏移：动作概率和状态访问概率。Token级别方法只校正了第一个。

真实梯度（g_{\mathrm{seq}}）：期望是关于正确的目标FSDP分布下访问的状态的，\mathbb{E}_{s \sim d_{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}}}。
有偏梯度（g_{\mathrm{tok}}）：期望是关于不正确的behavior vLLM分布下访问的状态的，\mathbb{E}_{s \sim d_{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}}。

这隐式地假设状态占用比率是1，即 {d_{\textcolor{blue}{\pi^{\mathrm{train}}}}(s)} /{d_{\textcolor{red}{\pi^{\mathrm{infer}}}}(s)} = 1。这个假设在自回归模型中严重不成立；由于确定性转移，单个不同的token选择会导致状态轨迹完全发散。通过忽略这一点，g_{\mathrm{tok}}(\theta) 引入了一个大的、不可控的偏差。

来源2：奖励信号不匹配

第二个关键错误是token级别梯度用来自错误策略的奖励信号来加权更新。

真实梯度（g_{\mathrm{seq}}）：更新按目标FSDP策略的优势函数缩放，A^{\textcolor{blue}{\pi_{\theta}^{\mathrm{train}}}}，表示该策略下的期望未来奖励。
有偏梯度（g_{\mathrm{tok}}）：更新按behavior vLLM策略的优势函数缩放，A^{\textcolor{red}{\pi_{\theta}^{\mathrm{infer}}}}。

Target policy的梯度被属于behavior policy的奖励信号缩放。由于状态分布和奖励信号都存在根本性的不匹配，token级别梯度是一个有偏且理论上不成立的估计器。

这些理论表明，尽管token级别方法可能具有较低的方差，但梯度偏差仍然存在，可能导致训练不稳定——我们接下来的实验证实了这一预测。 我们还在(Part 1 & Part 2)中给出了token级别和sequence级别方法的详细偏差和方差分析。

实验验证

我们的理论分析预测有偏的token级别IS将是不稳定的并最终失败，而无偏的sequence级别IS将是稳健的。我们的实验证实了这一点。

IS防止梯度爆炸，但Token级别仍然失败

我们从L20 GPU上崩溃实验的第200个训练步骤恢复，分别使用token级别TIS和sequence级别TIS（C=2）。如图14所示，虽然两者最初都防止了朴素实验中看到的梯度爆炸，但使用token级别TIS的运行后来仍然崩溃。使用sequence级别TIS的运行保持稳定，验证了我们的理论，即token级别方法的有偏梯度最终导致失败。

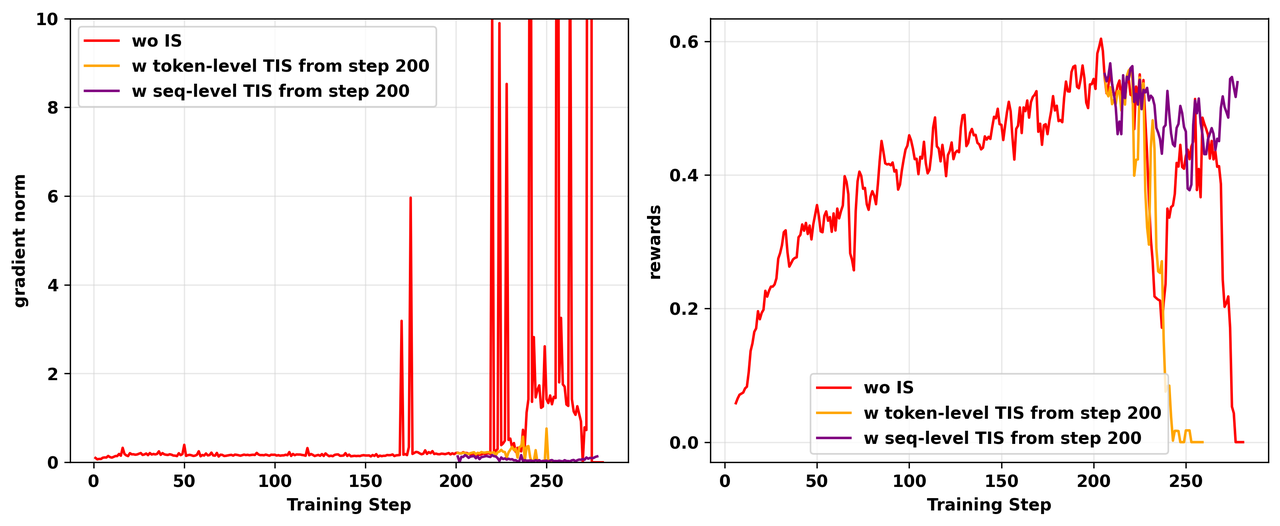
image 16-PsWQ.png

图14: 不同TIS策略使用的消融研究。不使用IS的朴素on-policy实验在200步后崩溃并经历梯度爆炸。我们分别从第200个训练步骤开始，添加token级别TIS和sequence级别TIS*策略恢复RL训练。左：RL训练期间gradient norm的动态。右：RL训练期间训练奖励的动态。*

reasoning RL中的Token级别TIS

虽然token级别TIS在我们复杂的TIR实验中失败，但在更简单的reasoning RL中它可以帮助防止崩溃，因为那里的不匹配程度较小。在on-policy GRPO和RLOO实验中（图15），token级别TIS防止了梯度爆炸，但训练仍然不稳定，没有达到更好的最终性能，这可能是由于底层的梯度偏差。

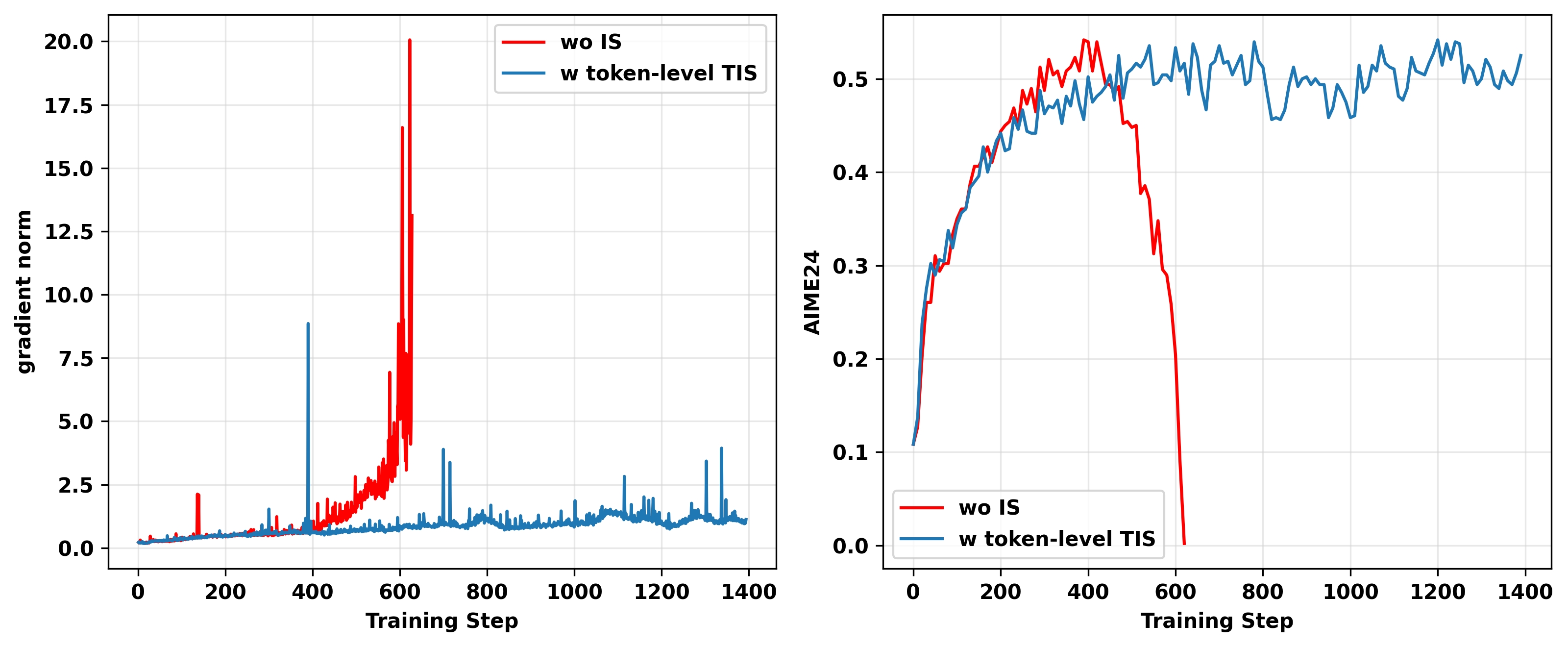
img_v3_02q6_c62b54ca-eaa5-4519-95ef-652e3b2fa0eg-uAyd.jpg

图15(a): H100 GPU上on-policy GRPO实验的gradient norm（左）和AIME 24准确率（右），分别为无IS和有token级别IS（C=2）的reasoning RL。Token级别TIS防止训练崩溃但没有达到更好的测试性能。

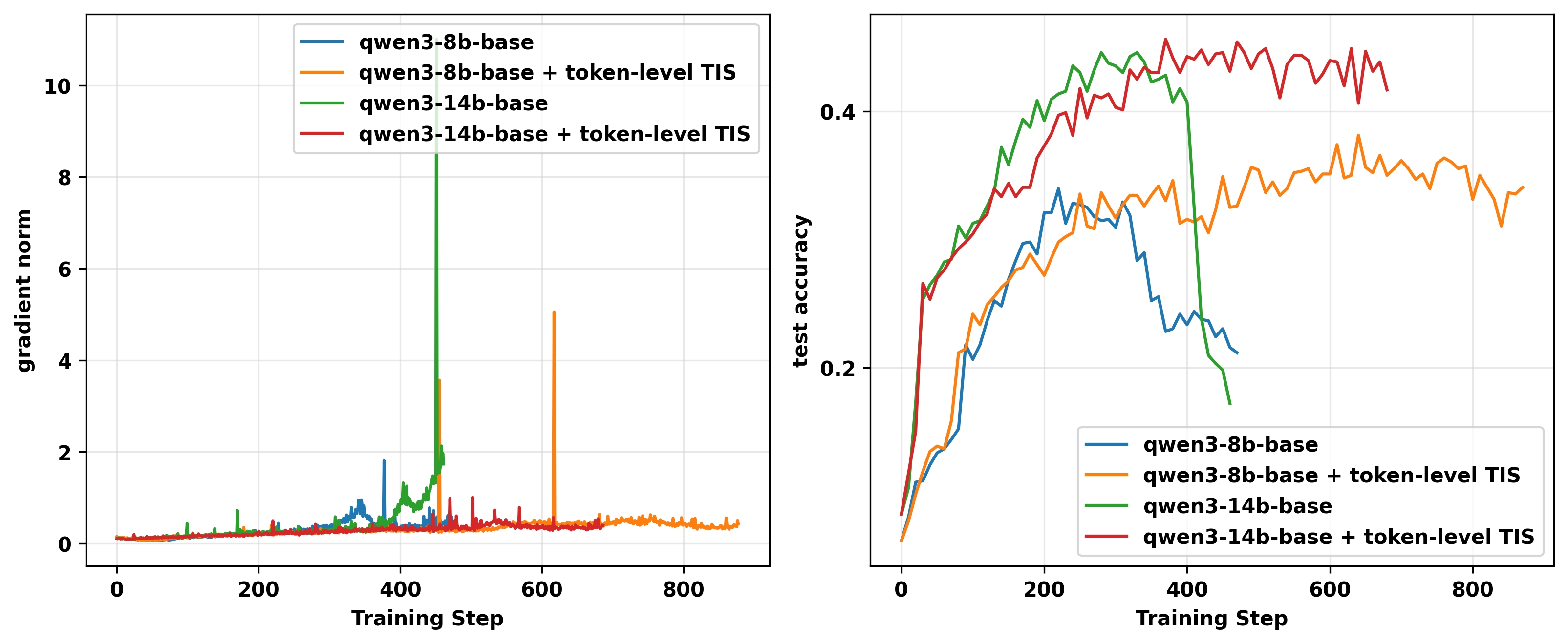
img_v3_02qd_87d5ed2e-e1f2-4b43-9eb5-d52ad649685g-TpcJ.jpg

图15(b): H100 GPU上on-policy RLOO实验的gradient norm（左）和AIME 24/AIME25平均准确率（右），分别为无IS和有token级别IS（C=2）的reasoning RL。Token级别TIS缓解训练崩溃但没有达到更好的测试性能。在后期阶段，TIS有性能下降的趋势。

TIS延长训练但可能遭受不稳定性

我们在L20 GPU上从头开始进行on-policy TIR实验，使用sequence级别TIS（C=2）。如图16所示，虽然该方法防止了完全崩溃，但奖励曲线在达到平台后表现出持续波动，其测试性能没有超过朴素实验崩溃前达到的峰值。

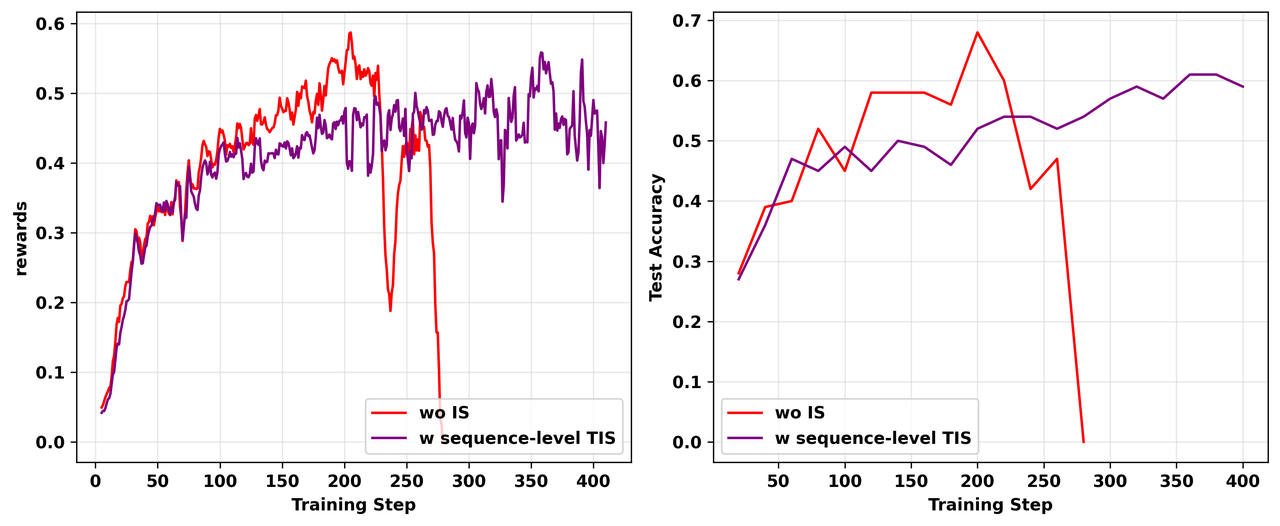
image 17-KnlA.png

图16: 不同TIS策略使用的消融研究（续）。不使用IS的朴素on-policy实验在200步后崩溃。我们从头开始使用相同配置重新运行失败的实验，添加 C=2 的sequence级别TIS。左：RL训练期间训练奖励的动态。右：RL训练期间测试准确率的动态。

掩码重要性采样（MIS）

为改进TIS，我们提出掩码重要性采样（Masked Importance Sampling，MIS），它对IS比率超过阈值 C 的序列掩盖策略损失（即 \rho(y|x) \gets \rho(y|x) \mathbb{I}\{\rho(y|x) \le C\}）。如图17所示，MIS不仅稳定了训练，还超过了朴素和TIS实验的峰值训练奖励和测试准确率。

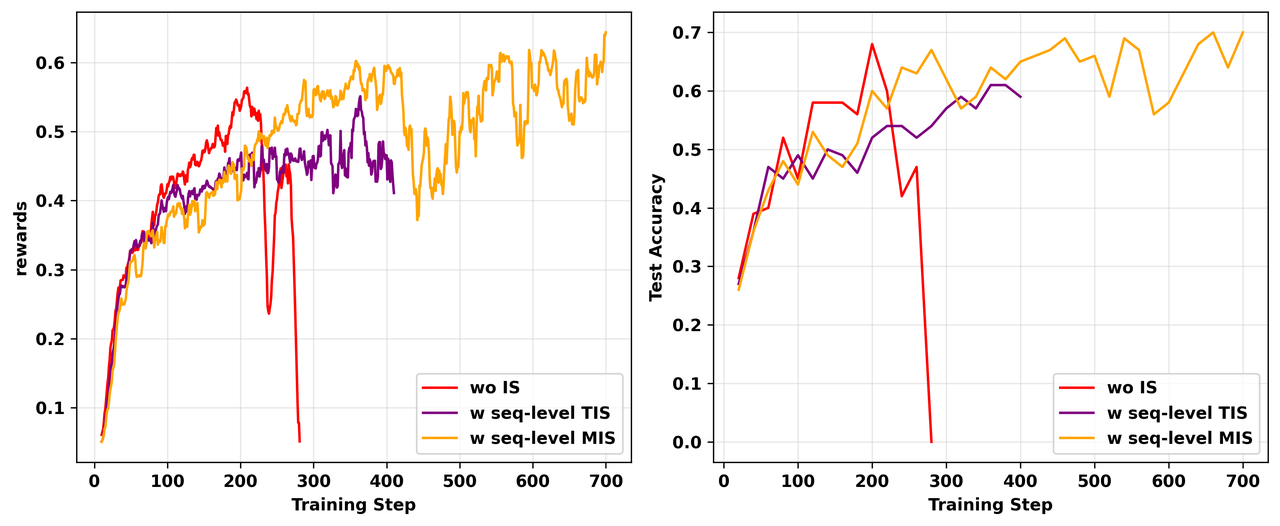
image 18-pIoq.png

图17: on-policy GRPO与sequence级别MIS、TIS和不使用IS的朴素版本的比较。所有三个实验都在L20 GPU上进行。与朴素on-policy实验相比，MIS和TIS的引入都延长了训练持续时间，但两者在后期阶段也遭受了训练不稳定性。与TIS相比，MIS在训练奖励和测试集准确率上都有所改进，也超过了不使用IS的朴素实验的峰值性能。左：RL训练期间训练奖励的动态。右：RL训练期间测试准确率的动态。

Token级别MIS vs. sequence级别MIS

最后，我们比较了token级别MIS和sequence级别MIS。如预期，图18显示虽然两者都防止了初始的梯度爆炸，但token级别MIS实验仍然崩溃。这强化了我们的结论：对于复杂的、长时间范围的自回归任务，只有理论上成立的sequence级别校正才是可靠的。

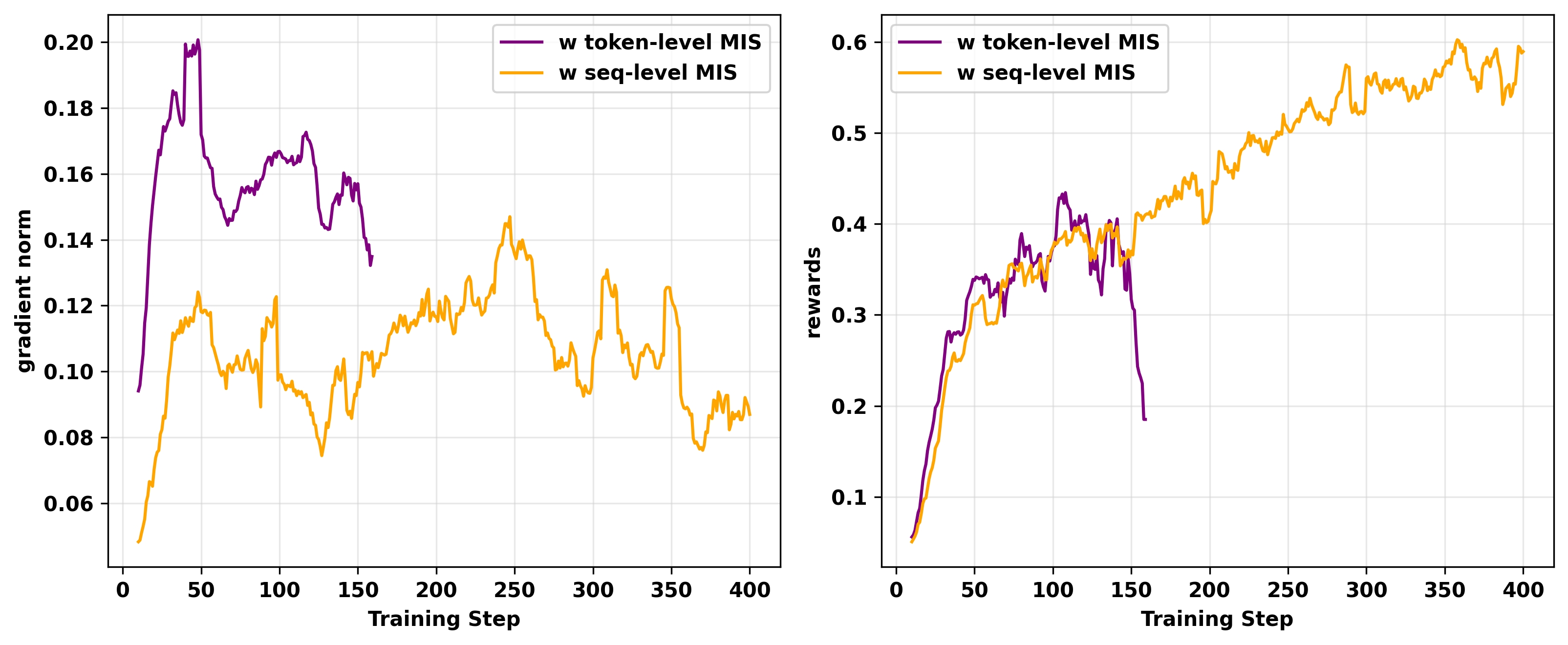
img_v3_02qb_d5ff66e7-2585-4275-a6f7-db4a65fbe60g-talz.jpg

图18: on-policy GRPO与token级别MIS和sequence级别MIS的比较。两个实验都在L20 GPU和相同配置上进行。左：RL训练期间gradient norm的动态。右：RL训练期间训练奖励的动态。

4.2.2 Top-p采样

如上所述，我们观察到vLLM策略的低概率token更容易出现严重的训练-推理不匹配问题，导致FSDP策略的概率极低。为进一步证实这一点，我们进行了以下top-p消融研究。

我们在L20 GPU上运行on-policy GRPO实验，将vLLM采样策略的 top-p超参数分别设置为0.98、0.99和0.999（注意我们没有应用重要性采样进行梯度校正）。通过设置较小的 top-p值，我们旨在减少推理阶段极低vllm概率token的频率，从而缓解训练-推理不匹配。我们的消融结果如图19所示。

如预期，vllm-kl指标表明较小的 top-p减少了 vllm-kl尖峰的发生。然而，需要注意的是，较小的 top-p也增加了vLLM策略 \textcolor{red}{\pi^{\text{infer}}_\theta} 和FSDP策略 \textcolor{blue}{\pi^{\text{train}}_\theta} 之间的分布差异。因此，在不应用TIS的情况下，梯度偏差变得更大，导致随着 top-p减小，奖励改进更慢。

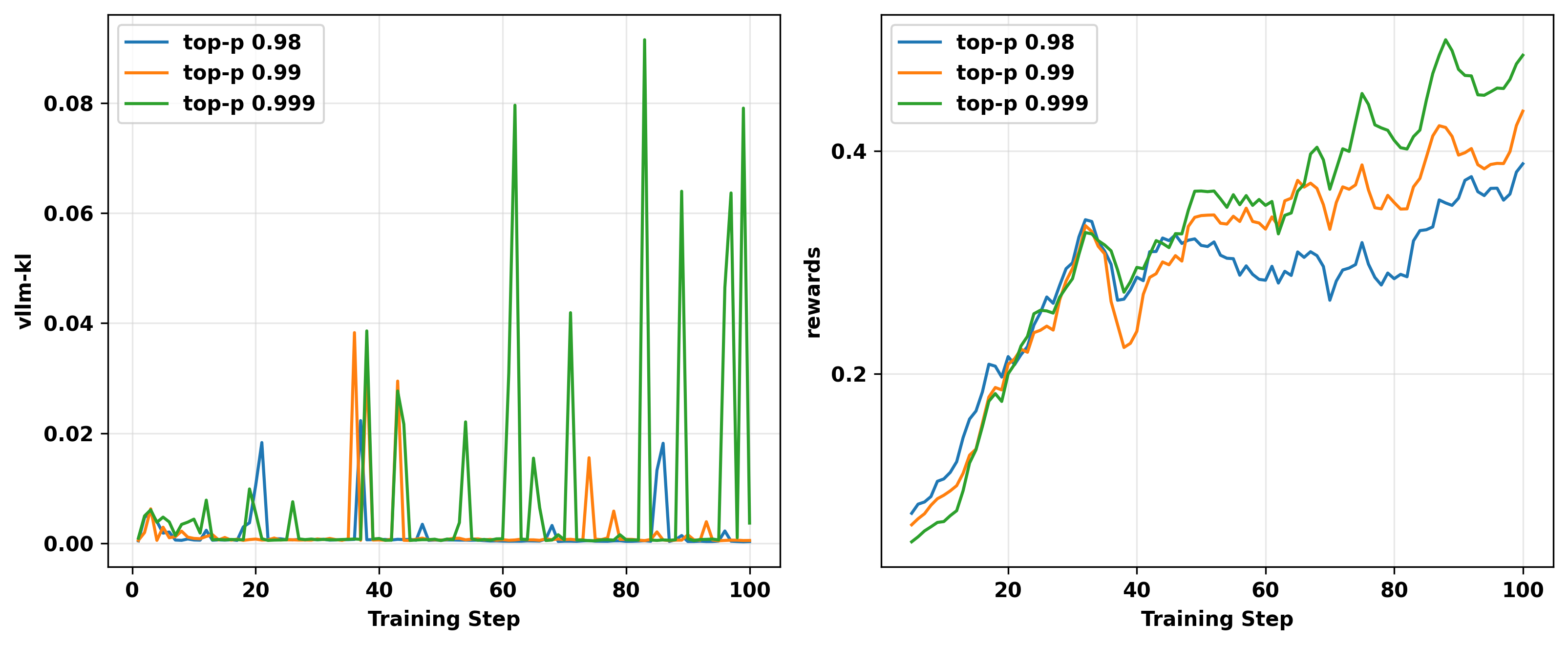
image 19-uCTg.png

图19: RL训练期间 vLLM 采样策略中不同 top-p值使用的消融研究。我们运行了 top-p分别等于0.98、0.99和0.999的on-policy GRPO实验。可以观察到，设置较小的 top-p值通常产生较小的 vllm-kl指标和较慢的奖励改进。左：RL训练期间 vllm-kl指标的动态。右：RL训练期间训练奖励的动态。

4.2.3 使用其他GPU系列

在发现H20 GPU上运行的实验中训练-推理不匹配显著小于L20 GPU后，我们将所有TIR实验切换到H20 GPU，这大大减少了训练崩溃的发生。图20展示了在相同配置下分别在L20和H20 GPU上从头训练的两个on-policy GRPO实验的结果。

可以观察到，在H20 GPU上运行的on-policy实验显著延长了稳定训练持续时间并取得了更好的性能。

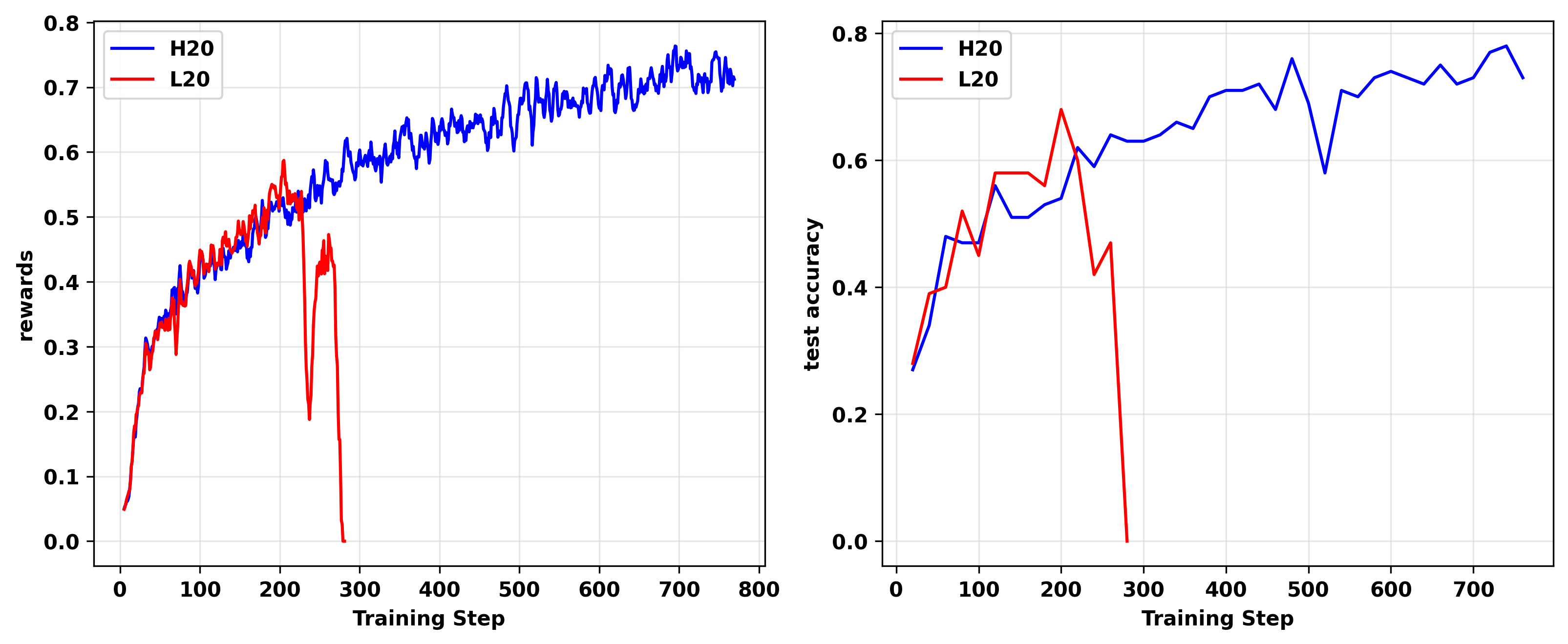
image 20-wUdI.png

图20: 分别在L20和H20 GPU上进行的两个on-policy GRPO实验的训练奖励（左）和测试准确率（右）。

4.2.4 在vLLM中禁用级联注意力

根据这个GitHub issue，我们在初始化vLLM引擎时设置 disable_cascade_attn=True，发现它显著帮助减少在A100 GPU上进行的实验中的训练-推理不匹配。

我们使用Qwen3-14B-Base作为基础模型在A100 GPU上进行了两个on-policy GRPO实验，disable_cascade_attn分别设置为 True和 False。结果如图21所示。

可以观察到，禁用级联注意力后，vllm-kl指标从5e-2到1e-1的范围下降到1e-3左右，表明训练-推理不匹配大幅减少。此外，训练集上的奖励也相应增加。

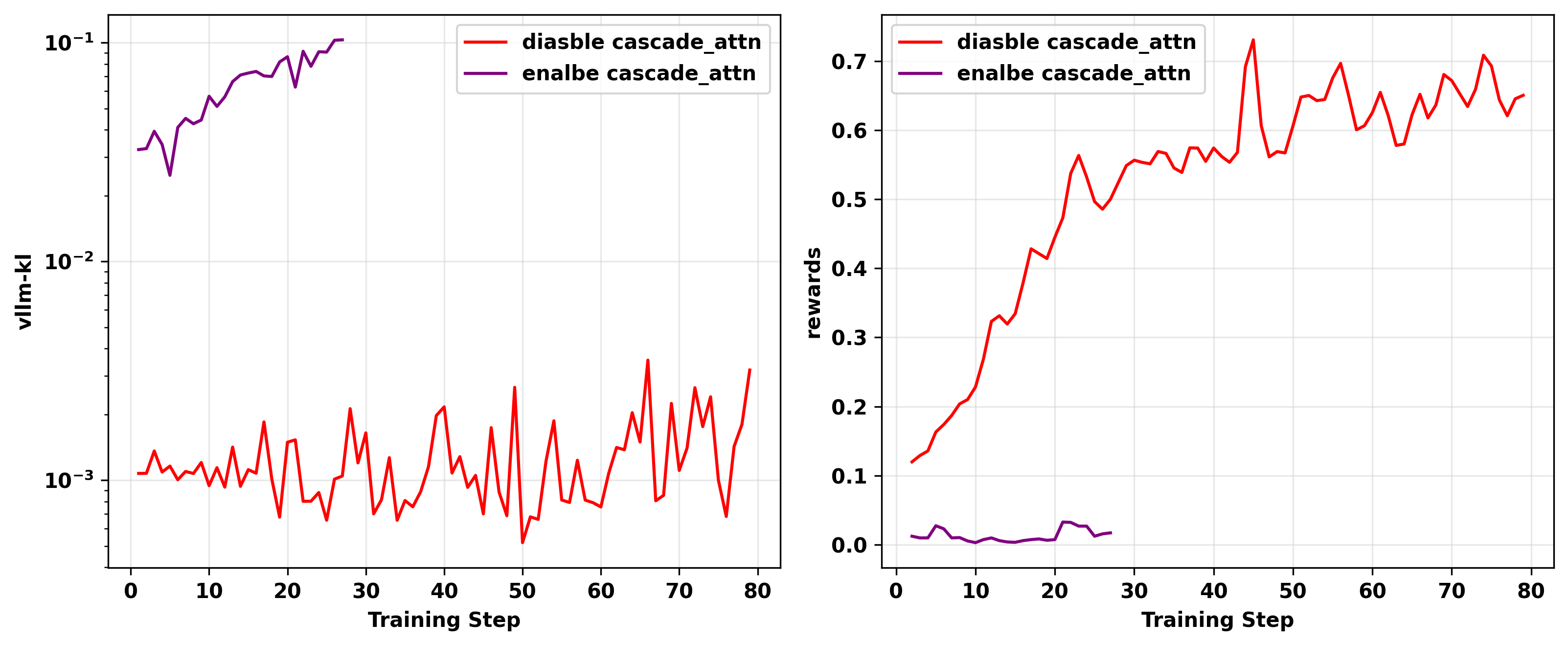
image 21-HwhE.png

图21: 使用级联注意力的消融研究结果。我们在A100 GPU上进行了两个on-policy实验：一个启用级联注意力，另一个使用相同配置但禁用级联注意力。左：vllm-kl指标的动态。右：训练奖励的动态。

5. 结论与实践者要点

训练-推理不匹配不是一个小众bug，而是现代reasoning和agent RL中一个根本性的、日益严峻的挑战，源于对性能的必然追求。我们的研究为诊断和缓解这一问题提供了清晰的路线图。

1、 不匹配是不可避免的权衡： 高速推理将始终与训练计算存在差异。这是核心权衡，而非临时缺陷。

2、 监控系统健康状态： train-infer-kl/vllm-kl指标是一个重要的早期预警系统。将它与困惑度（PPL）和梯度范数一起跟踪，以在崩溃发生之前预测和诊断不稳定性。

3、 识别问题根源： 问题并非随机发生。它被低概率token系统性地触发，而当模型处理分布外（OOD）输入时，这些token会更频繁地生成——这是tool-use和多轮应用中的常见场景。

4、 硬件是一阶变量： 相同的代码可能在一个GPU架构上崩溃而在另一个上完美训练。务必在目标硬件上验证你的设置，因为结果可能无法完全移植。

5、 使用理论上可靠的校正方法： 虽然更换硬件或调整采样器可以有所帮助，但最稳健且有原理依据的解决方案是算法性的。我们的工作证明了理论上有偏的token级别校正是不够的，在我们的实验中仍然可能失败。

相比之下，sequence级别方法如截断重要性采样（Seq-TIS）和掩码重要性采样（Seq-MIS） 通过校正完整的状态轨迹直接解决梯度偏差。这些方法对于保持稳定性至关重要，应该被视为任何严肃的LLM-RL训练栈的默认配置。

我们假设推理引擎（如vLLM）和训练框架（如Megatron-LM）之间的这种不匹配对于混合专家模型（MoE）RL也将是一个重要问题，这代表了一个有趣且关键的未来研究方向。

当速度扼杀稳定性：字节揭秘训练-推理不匹配导致的RL崩溃

最新动态