作者：kxzxvbk

原文：https://zhuanlan.zhihu.com/p/2000612721868177979

最近，越来越多 LLM 相关的工作提到了一个关键词 On-Policy Distillation （后文会简称为 OPD），这个方法迅速受到大家的广泛追捧和好评。

本文将从 OPD 的核心做法和 idea 出发，再介绍一些基于 OPD 的最新工作，主要聚焦于自蒸馏 self-disdillation。希望能快速对这个领域有大致的认识。

On-Policy Distillation 的核心思想

随着对强化学习（RL）的不断研究，研究者逐渐发现强化学习最大的好处，或许在于它 on-policy 的特性。所谓 on-policy，指的就是模型的学习内容是自己 rollout 出来的好的样本。这样做的好处有很多，举一些例子：

这样的模型不容易出现灾难性遗忘的问题。RL 的训练目标是“强化”自身生成的好的样本，而不是强行去拟合新的数据分布，对模型内部的知识不会产生破坏效果。

真正 inference 的时候会更加鲁棒。少量的 SFT 样本，只能教会模型强行记住某一条轨迹（A -> B -> C），但是一旦中途发生了些许扰动（如 A -> B' -> ?），模型由于缺乏对轨迹的深入理解，就可能就会发生错乱。

但是 RL 也有它固有的问题，就是计算不够高效，每次 rollout 一条 trace，都只能获得一个最终的奖励信号。而对比 SFT，对于每一个 token，都有一个对应的 label 来约束更新。这样相比起来，RL 在训练中，模型从一次尝试中学到的内容太少了，效率较低。

那么，能不能有一种方法，既具有 on-policy 的特征，又能像 SFT 那样，对每个 token 都加以监督呢？本文的主角 OPD 就是一个有效的尝试，引入蒸馏的思想来解决这个问题。

核心的思想很简单，首先由 student model 来 rollout 样本（体现了 on-policy 特点）；然后用 teacher model 计算每个 token 对应的 logit；最后拉进 student 和 teacher 在每个 token 上的 logit 分布即可（体现了蒸馏）。

具体到实现方式层面，我们简单介绍几种常见的实现。按照Thinking Machine Lab 的实现，OPD 本质上就是通过采样的方法，优化模型策略 \pi_{\theta} 和教师策略 \pi_{teacher} 之间的 reverse KL，也就是：

\mathrm{KL}\!\left(\pi_\theta \,\middle\|\, \pi_{\text{teacher}}\right) = \mathbb{E}_{x \sim \pi_\theta} \left[ \log \pi_\theta\!\left(x_{t+1} \mid x_{1..t}\right) - \log \pi_{\text{teacher}}\!\left(x_{t+1} \mid x_{1..t}\right) \right]. \quad\quad (1)

在实操的时候也很简单，首先使用需要训练的模型 \pi_{\theta} 进行 rollout；然后再使用上面右侧的公式计算出 logit 距离 teacher 的距离作为损失函数；最后梯度下降进行计算就可以了。

上面这个方案理论上没有毛病，但是事实上对于每一个 token，只用到了一个 logit 维度的信息进行蒸馏，监督的信息还有增加空间。因此，一个 paper 中常见的技巧是将词表的每一维度信息都利用起来，更好地估计上述 KL 散度的梯度，也就是：

\nabla_\theta \mathrm{KL}\!\left(\pi_\theta \,\middle\|\, \pi_{\text{teacher}}\right) = \mathbb{E}_{x \sim \pi_\theta} \left[ \sum_t \sum_{x_t \in \mathcal{V}} \log \frac{\pi_\theta \left(x_{t+1} \mid x_{1..t}\right)} {\pi_{teacher} \left(x_{t+1} \mid x_{1..t}\right)} \, \nabla_\theta \log \pi_\theta \!\left(x_{t+1} \mid x_{1..t}\right) \right]. \quad\quad(2)

其中， V 指的是模型的词表。以上就是 OPD 的核心方法，整体还是相当简洁的。

从 OPD 到 self-distillation

OPD 单纯的方法部分已经相当简洁有效了，感觉可优化的空间不大，唯独不好处理的点在于 teacher model 怎么获得。

如果按照一般的想法，teacher model 使用一个 size 很大的开源模型，那么 tokenizer 很可能和 student model 不一致，那么蒸馏的 logit 和位置就对不齐，直接导致方法用不了；另一方面，虽说做实操我们总喜欢蒸馏更强的模型（不是），但做科研我们总是想提高模型的上限，那么简单的蒸馏就做不到这点了。

所以最近看到不少 paper 都采用了 self-distillation 的思想，也就是自己蒸馏自己 —— 这样就避免了 tokenizer 不统一的问题。这类工作的核心问题在于，怎么让自己 rollout 更好的结果，作为 teacher。

因此不少文章给出了解决方案 [1][2]：可以在模型输入的 prompt 里面，把专家的解答过程（demonstration）放进去，并让模型基于专家答案，给出解答过程。这样一来，能保证最终 rollout 的质量，又能保证 on-policy 的特点。写成公式的形式，teacher 模型的策略就是：（c 是专家给出的答案）

\pi_{teacher}(y\mid x) = \pi_{\theta}(y\mid x,c). \quad\quad (3)

这个思想从某种程度来说，是将专家数据用自己的模型进行改写，成为和符合自己模型风格的样本，后续再进行训练和监督。这样就能取得更好的效果。

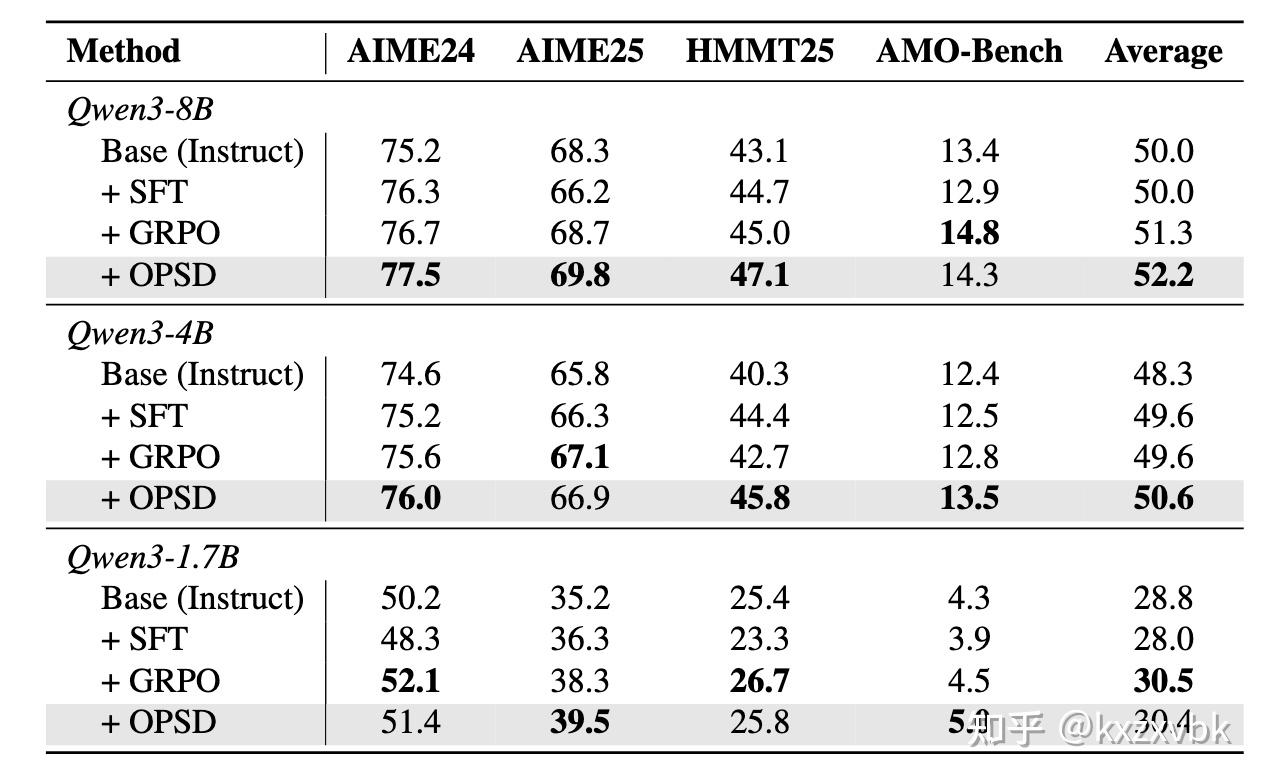
从结果上来看，自蒸馏的方法，也确实同时兼备了 SFT 丰富监督信号的优点 + RL on-policy 的优点，在实验中表现出了比二者都要更好的效果。

OPSD 为自蒸馏方法

参考文献

[1] Self-Distilled Reasoner: On-Policy Self-Distillation for Large Language Models.
https://arxiv.org/abs/2601.18734
[2] Self-Distillation Enables Continual Learning.
https://arxiv.org/abs/2601.19897``````

On-Policy Distillation 是什么？如何做？

On-Policy Distillation 的核心思想

从 OPD 到 self-distillation

参考文献