作者:catneverfat
https://zhuanlan.zhihu.com/p/1908671543476749557
PPO是一种被广泛应用于各个场景下的强化学习算法,笔者之前对它展开过介绍。但是当时主要的理论推导集中在Policy Gradient部分,对PPO主要介绍的是它的目标函数以及训练的流程,其实并没有涉及它的目标函数为什么是那样。
有读者阅读比较深入的话,其实也还会发现,PPO的目标函数与Reinforce算法的目标函数还是有一定差异的,尤其是它采用了 \pi_{\theta_{old}} 来采样数据并在目标函数中引入重要性采样 \frac{\pi_{\theta}}{\pi_{\theta_{old}}} 。
这其实并不直观,我们明明推导的是基于蒙特卡洛采样的Policy Gradient
怎么目标函数中有这么多不同的策略网络呢?
为什么采样的策略和执行更新的策略不一样呢?
为什么长得这么不一样的目标函数也可以算作蒙特卡洛采样呢?
这篇文章就要来梳理这个问题,首先从TRPO说起。
TRPO(Trust Region Policy Optimization)和PPO(Proximal Policy Optimization)的作者是同一人,TRPO也是PPO的前身工作。
策略梯度优化目标
基于策略梯度的推导,我们有策略的优化目标为:
\nabla_{\theta}J(\pi_{\theta})=E_{\tau\sim\pi_{\theta}}[\sum_{i=0}^T\nabla_{\theta}\log\pi_{\theta}(a_i|s_i)\cdot R(\tau)]
基于蒙特卡洛法采样,可以对策略梯度进行估计:
\hat g=\frac{1}{D}\sum_{\tau\in D}\sum_{t=0}^T\nabla_{\theta}\log\pi_{\theta}(a_t|s_t)R(\tau)
为了减少方差,一般引入优势函数,于是,优化目标变为:
\nabla_{\theta}J(\theta)\approx \frac{1}{N}\sum_{i=1}^{N}\sum_{t=0}^{T}\nabla_{\theta}\log\pi_{\theta}(a_{i,t}|s_{i,t})A^{\pi}(s,a)
其中
A^{\pi}(s,a)=Q^{\pi}(s,a)-V^{\pi}(s)=r(s_t,a_t)+\gamma V^{\pi}(s_{t+1})-V^{\pi}(s)
TRPO前置工作
强化学习过程表述:
对于无限长的马尔科夫过程(MDP), 它可以用一系列元组来表示, (\mathcal{S}, \mathcal{A}, P, r, \rho_0, \gamma ), 其中
\mathcal{S} 代表状态集合, \mathcal{A} 代表动作集合,
\mathcal{P}:S\times A\times S \rightarrow \mathbb{R}
代表状态转移方程,
r: S\rightarrow\mathbb{R}
代表奖励函数,
\rho_0: S \rightarrow \mathbb{R} 是初始状态分布, \gamma \in (0,1) 代表折扣因子。
对于一个随机策略
\pi : \mathcal{S} \times \mathcal{A} \rightarrow [0, 1]
, 定义它期望回报为
\eta(\pi) = \mathbb{E}_{s_0, a_0, \dots} \left[ \sum_{t=0}^{\infty} \gamma^t r(s_t) \right],\\ (s_0 \sim \rho_0(s_0),\ a_t \sim \pi(a_t | s_t),\ s_{t+1} \sim P(s_{t+1} | s_t, a_t)).
强化学习中,标准的动作-状态价值,状态价值和优势函数被表述为:
Q^{\pi}(s_t, a_t) = \mathbb{E}_{s_{t+1}, a_{t+1}, \dots} \left[ \sum_{l=0}^{\infty} \gamma^l r(s_{t+l}) \right],
\\ V^{\pi}(s_t) = \mathbb{E}_{a_t, s_{t+1}, \dots} \left[ \sum_{l=0}^{\infty} \gamma^l r(s_{t+l}) \right]
\\ A^{\pi}(s, a) = Q^{\pi}(s, a) - V^{\pi}(s)
\\ (a_t \sim \pi(a_t | s_t),\ s_{t+1} \sim P(s_{t+1} | s_t, a_t).
引理一 : 对于任意两个不同策略 \tilde\pi,\pi ,有
\begin{equation} \eta(\tilde{\pi}) = \eta(\pi) + \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum_{t=0}^{\infty} \gamma^t A^{\pi}(s_t, a_t) \right] \tag{1} \end{equation}
其中, \eta(\pi) 代表该策略的性能,也就是期望回报。
证明 :
\begin{align*} \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum_{t=0}^\infty \gamma^t A_\pi(s_t, a_t) \right] &= \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum_{t=0}^\infty \gamma^t \left( r(s_t) + \gamma V_\pi(s_{t+1}) - V_\pi(s_t) \right) \right] \\ &= \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ -V_\pi(s_0) + \sum_{t=0}^\infty \gamma^t r(s_t) \right] (裂项相消)\\ &= -\mathbb{E}_{s_0} \left[ V_\pi(s_0) \right] + \mathbb{E}_{\tau \sim \tilde{\pi}} \left[ \sum_{t=0}^\infty \gamma^t r(s_t) \right] \\ &= -\eta(\pi) + \eta(\tilde{\pi}) \end{align*}
如果让
\rho_{\pi}(s)=P(s_0=s)+\gamma P(s_1=s)+\gamma^2P(s_2=s)+\cdots
把
\rho_{\pi}(s)
定义为状态s的访问频率,那么根据引理一有:
\begin{equation}
\begin{aligned}
\eta(\tilde{\pi})
&= \eta(\pi) + \sum_{t=0}^{\infty} \sum_s P(s_t = s \mid \tilde{\pi})
\sum_a \tilde{\pi}(a \mid s) \gamma^t A_\pi(s, a) \\
&= \eta(\pi) + \sum_s \sum_{t=0}^{\infty} \gamma^t
P(s_t = s \mid \tilde{\pi})
\sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) \\
&= \eta(\pi) + \sum_s \rho_{\tilde{\pi}}(s)
\sum_a \tilde{\pi}(a \mid s) A_\pi(s, a)
\end{aligned}
\tag{2}
\end{equation}
这个式子告诉我们,在训练时进行参数更新,让 \pi \rightarrow \tilde{\pi} 时,如果每一个状态的期望优势 \sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) \ge 0 , 那么新策略 \tilde{\pi} 的性能(即预期回报)一定大于等于旧策略,也就是它会是一个单调不减的过程。
那么我们只需要在训练过程中,取 \tilde{\pi}(s) = \arg\max_a A_π(s, a) ,那么在至少有一个动作-状态对的优势大于0并且相应的访问概率不为0的情况下,模型性能都可以提升。
但是呢,这只是理想情况下,在真实训练过程中,由于我们进行了采样估计,不可避免地会采集到 \sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) \le 0 的状态,那么这种单调不减的特性就会被打破,从而不能保证新策略一定好于旧策略,整个优化过程可能就不够稳定。
对于这种情况,我们希望对其进行约束。在新策略的目标(2)式中, \rho_{\tilde{\pi}}(s) 是一个不好控制的项(因为它依赖于我们的新策略 \tilde{\pi} ,而它是我们的优化目标),所以要想办法把它替换成我们的已知项或已有项。可以定义局部近似函数:
L_\pi(\tilde{\pi}) = \eta(\pi) + \sum_s \rho_\pi(s) \sum_a \tilde{\pi}(a \mid s) A_\pi(s, a) \tag{3}
从而把 \rho_{\tilde{\pi}}(s) 换成了 \rho_{{\pi}}(s) 。将这个式子作为我们的优化目标可以给出一个更清晰的优化路径。
这里之所以可以这样做的原因是,如果 \pi_{\theta}(a|s) 是参数网络 \theta 的可微分方程,那么对于任何的给定的参数网络 \theta_{0} , L_{\pi} 都与 \eta(\pi) 有直到一阶导数的匹配关系(暂时只给出结论,省略证明略 ),即:
L_{\pi_{\theta_0}}(\pi_{\theta_0}) = \eta(\pi_{\theta_0}), \quad \nabla_\theta L_{\pi_{\theta_0}}(\pi_\theta)\big|_{\theta = \theta_0} = \nabla_\theta \eta(\pi_\theta)\big|_{\theta = \theta_0} \tag{4}
也就是说,在一个 L_{\pi}(\tilde\pi) 与 \eta({\tilde\pi}) 在 \pi 点的一阶导数是相等的,那么对 L_{\pi}(\tilde\pi) 进行梯度下降优化是与 \eta({\tilde\pi}) 进行梯度下降优化是等效的。当然,这里的前提条件是 \tilde\pi 与 \pi 的分布足够接近。
那么问题来了,多近算近呢?这个局部近似函数并不能指导我们以多大的步幅去进行策略的更新。
Kakade and Langford提出过一种保守策略迭代的方法(conservative policy iteration,CPI)。用 \pi_{old} 表示当前的采样策略,
\pi'=\arg\max_{\pi'}L_{\pi_{old}}(\pi')
,更新的策略 \pi_{new} 则可以被定义为:
\pi_{\text{new}}(a \mid s) = (1 - \alpha) \pi_{\text{old}}(a \mid s) + \alpha \pi'(a \mid s) \tag{5}
相对应地推导出了如下的下界:
\begin{equation}
\begin{aligned}
\eta(\pi_{\text{new}})
&\geq L_{\pi_{\text{old}}}(\pi_{\text{new}})
- \frac{2 \epsilon \gamma}{(1 - \gamma)^2} \alpha^2 \\
\\
\text{其中}\quad
\epsilon
&= \max\limits_s
\left|
\mathbb{E}_{a \sim \pi'(a \mid s)}
\left[ A_{\pi}(s, a) \right]
\right|
\end{aligned}
\tag{6}
\end{equation}
这个式子告诉了我们,只要以一定幅度 \alpha 更新策略,那么新策略的性能相对于局部近似函数是有一个下界保证的。
但是呢,这个下界只在策略是如(5)式的线性组合时才成立,要对任意随机策略进行优化的话,这个方法是不足够的。
TRPO推广
TRPO注意到式(6)可以被修改并推广到任意随机策略。定义两个离散概率分布 q,p 的Total Variation Distance为
D_{TV}(p||q)=\frac{1}{2}\sum\limits_i|p_i-q_i|
那么
D_{TV}^{max}(\pi,\tilde{\pi})=\max\limits_sD_{TV}(\pi(\cdot|s)||\tilde{\pi}(\cdot|s))
令
\alpha=D_{TV}^{max}(\pi_{old},\pi_{new})
,则以下不等式成立(证明暂略):
\begin{equation} \eta(\pi_{\text{new}}) \geq L_{\pi_{\text{old}}}(\pi_{\text{new}}) - \frac{4 \epsilon \gamma}{(1 - \gamma)^2} \alpha^2\\ \text{where} \quad\epsilon = \max\limits_{s,a} \left| A^{\pi}(s, a) \right|\tag{7} \end{equation}
又由于
D_{\mathrm{TV}}(p \,\|\, q)^2 \leq D_{\mathrm{KL}}(p \,\|\, q)
让
D^{\max}_{\mathrm{KL}}(\pi, \tilde{\pi}) = \max_s D_{\mathrm{KL}}\left( \pi(\cdot \mid s) \,\|\, \tilde{\pi}(\cdot \mid s) \right)
则有:
\begin{equation} \eta(\tilde{\pi}) \geq L_{\pi}(\tilde{\pi}) - C \cdot D^{\max}_{\mathrm{KL}}(\pi, \tilde{\pi})\\ \text{where}\quad C = \frac{4 \epsilon \gamma}{(1 - \gamma)^2}\tag{8} \end{equation}
让
M_i(\pi) = L_{\pi_i}(\pi) - C \cdot D^{\max}_{\mathrm{KL}}(\pi_i, \pi)
根据(8) \eta(\pi_{i+1}) \geq M_i(\pi_{i+1}) , 而 \eta(\pi_i) = M_i(\pi_i) , 所以有:
\eta(\pi_{i+1}) - \eta(\pi_i) \geq M_i(\pi_{i+1}) - M_i(\pi_i)
这就意味着,只要我们持续令 M_i(\pi_{i+1}) \geq M_i(\pi_i) ,就可以保证,新策略的预期回报单调不减。也就是说,我们得到了一个更容易优化的优化函数(surrogate objective) M_i ,优化它可以保证目标函数被同步优化,从而得到一系列单调不减的
\eta(\pi_0)\leq\eta(\pi_1)\leq\eta(\pi_2)\cdots\leq\eta(\pi_n)
这实际上是经典的MM算法。
TRPO
根据式(8)和Algorithm (1),我们可以得到一个目标函数的一个整体优化流程。但是这个算法在很多场景下并不实用。首先,
\epsilon = \max\limits_{s,a} \left| A^{\pi}(s, a)\right|
对于无限状态空间的问题的话,这个 \epsilon 所需的max是很难得到的。同样的
D^{\max}_{\mathrm{KL}}(\pi, \tilde{\pi}) = \max_s D_{\mathrm{KL}}\left( \pi(\cdot \mid s) \,\|\, \tilde{\pi}(\cdot \mid s) \right)
这里的最大KL散度也是很难得到的。而即便得到了这些条件,策略更新的幅度也只能非常小。为了能够稳健地用更大的幅度去更新策略,可以采用Trust Region 的约束,即:
\begin{equation}
\begin{aligned}
\max_{\theta} \quad
& L_{\theta_{\text{old}}}(\theta) \\
\text{subject to} \quad
& D^{\max}_{\mathrm{KL}}(\theta_{\text{old}}, \theta) \leq \delta
\end{aligned}
\tag{9}
\end{equation}
这里的KL散度还可以进一步不按照最大值去约束,而是变为平均KL散度约束(有利于采样估计):
\begin{equation}
\begin{aligned}
\max_{\theta} \quad
& L_{\theta_{\text{old}}}(\theta) \\
\text{subject to} \quad
& \bar D^{\rho_{\theta_{\text{old}}}}_{\mathrm{KL}}
(\theta_{\text{old}}, \theta) \leq \delta \\
\text{where} \quad
& \bar D^{\rho}_{\mathrm{KL}}(\theta_1,\theta_2)
:= \mathbb{E}_{s \sim \rho}
\!\left[
D_{\mathrm{KL}}
\!\left(
\pi_{\theta_1}(\cdot \mid s)
\,\|\,
\pi_{\theta_2}(\cdot \mid s)
\right)
\right]
\end{aligned}
\tag{10}
\end{equation}
TRPO采样估计(蒙特卡洛法):
重要性采样定理:
\begin{aligned}
\text{Given two probability distributions } p(x) \text{ and } q(x),
\text{ and a function } f(x), \\
\text{we want to estimate the expectation under } p: \quad
& \mathbb{E}_{x \sim p}[f(x)] \\
\text{If sampling from } p \text{ is difficult but sampling from } q \text{ is feasible,} \\
\text{we can use importance sampling:} \quad
& \mathbb{E}_{x \sim p}[f(x)]
= \mathbb{E}_{x \sim q}
\left[
\frac{p(x)}{q(x)} f(x)
\right]
\end{aligned}
根据(10),我们的优化目标为:
\begin{aligned} & \underset{\theta}{\text{maximize}} & & \sum_{s} \rho_{\theta_{\text{old}}}(s) \sum_{a} \pi_{\theta}(a|s) A_{\theta_{\text{old}}}(s, a) \\ & \text{subject to} & & \bar{D}_{\text{KL}}^{\rho_{\theta_{\text{old}}}}(\theta_{\text{old}}, \theta) \leq \delta \qquad \end{aligned}
通过重要性采样定理,选择一个采样分布 q ,
\sum\limits_s\rho
变成一个期望分布,那么这个目标可以写为:
\sum_{a} \pi_{\theta}(a \mid s_n) A_{\theta_{\text{old}}}(s_n, a) = \mathbb{E}_{a \sim q} \left[ \frac{\pi_{\theta}(a \mid s_n)}{q(a \mid s_n)} A_{\theta_{\text{old}}}(s_n, a) \right].
由于在期望下,某个状态的价值是与策略无关的常数,那么可以把优势A替换为动作-状态价值Q,从而得到:
\begin{equation}
\begin{aligned}
\max_{\theta} \quad
& \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}},\, a \sim q}
\left[
\frac{\pi_{\theta}(a \mid s)}{q(a \mid s)}
Q_{\theta_{\text{old}}}(s, a)
\right] \\
\text{subject to} \quad
& \mathbb{E}_{s \sim \rho_{\theta_{\text{old}}}}
\left[
D_{\mathrm{KL}}
\left(
\pi_{\theta_{\text{old}}}(\cdot \mid s)
\,\|\,
\pi_{\theta}(\cdot \mid s)
\right)
\right]
\leq \delta
\end{aligned}
\tag{11}
\end{equation}
式(14)就是TRPO最终推导得到的目标函数与约束条件,这个式子允许我们使用蒙特卡洛法采样轨迹进行策略更新。
行文至此,其实已经回答了文章开头所提出来的为什么可以用不同的策略进行采样和更新,PPO实际上就是在(11)的基础上提出了一些不一样的约束和惩罚,进行了一些工程上的优化,但是它优化目标的理论支撑,仍然来自(11)。
优化目标介绍至此,下面介绍TRPO提出的采样方法和策略优化过程。
采样方法
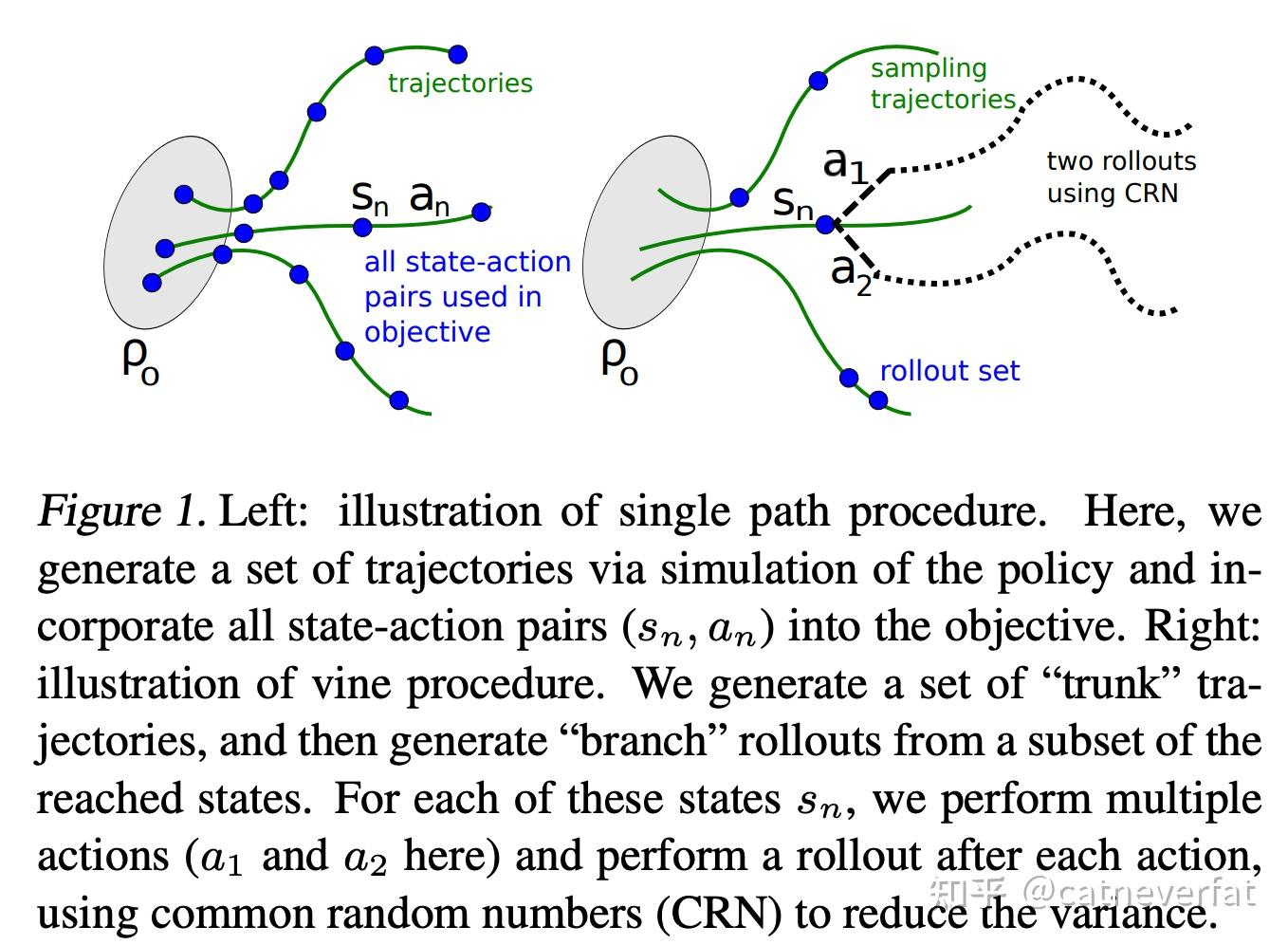
Single path:
采样一条路径,存储路径过程,用于策略更新,在此情况下,
q(a|s)=\pi_{\theta_{old}}(a|s)
。
Vine:
从 s_0\sim\rho_0 中采样多条路径,然后从这些路径上随机选择N个状态点 S_1,S_2\cdots S_N ,把这些状态点作为“roll-out”set,从这些状态点出发,通过 \pi_{\theta_{old}} 采集K个动作,那么每个状态对于策略网络更新的贡献为:
L_n(\theta)=\sum\limits_{k=1}^{K}\pi_{\theta}(a_k|s_n)\hat Q(s_n,a_k)
然后我们可以通过平均每个状态的贡献来对策略网络进行更新。
Vine通过多条路径的随机采样,可以有效地减小方差,但是呢,它需要系统可以从任意状态重新开始,要进行大量的reset来获取不同出发点的数据,并且要进行更多的价值估计计算。
训练过程
Use the single path or vine procedures to collect a set of state-action pairs along with Monte Carlo estimates of their Q-values.
By averaging over samples, construct the estimated objective and constraint in Equation (11)
Approximately solve this constrained optimization problem to update the policy’s parameter vector θ. We use the conjugate gradient algorithm followed by a line search, which is altogether only slightly more expensive than computing the gradient itself.
原文中采用了一些二阶估计,用于严格保证KL散度约束,用了海森矩阵,Fisher information矩阵什么的,用于梯度策略更新。
一般后续的算法没这么麻烦,直接使用Adam优化器用深度学习的标准流程就可以,这也是PPO后续摒弃的一点,它将严格的KL散度约束改为了KL散度补偿以及clip。
感兴趣的同学可以了解一下,详见原文Trust Region Policy Optimization 附录C,D部分。
小结:
这篇文章主要梳理了TRPO的目标函数,TRPO给出了一个有严格理论支撑的优化目标及其约束条件,后续的算法在此基础上做了一些工程上的改良,但是其实相应的弱化了TRPO提出的理论边界。
像PPO,更像是一个实验验证成功的算法,本身理论支撑并没有TRPO这么充分。