作者：初级程序员

https://zhuanlan.zhihu.com/p/1978480903136245222

本文面向已了解强化学习中策略梯度（policy gradient）、优势函数（advantage）、重要性采样（importance sampling）等概念的读者，重点对大模型强化学习主流算法做一条线的梳理与比较。

强化学习 (RL, Reinforcement Learning) 已成为大模型后训练必不可少的环节。本篇将介绍 PPO, GRPO, DAPO, GSPO, SAPO 等大模型主流强化学习算法，在此之前，我先简短回答几个问题，让大家对强化学习在大模型训练中有更直观、全面的认识：

一般情况下，强化学习训练前为何要先进行监督微调（SFT, Supervised Finetuning）？
为什么强化学习训练在大模型领域是重要的？

首先，大模型在前期会使用大量文本进行自监督（self-supervised）预训练（文字接龙），这个阶段决定了模型能力的上限，模型在过程掌握大量知识，但缺乏指令遵循能力。

此时，直接进行 RL 训练会导致大部分采样样本没有奖励信号，训练效率低下，为提高训练效率，SFT 训练能快速提升模型指令遵循的能力，提高 RL 阶段的训练效率。SFT 相当于 RL 训练前的 warm start。

这时大家会好奇，既然 SFT 能提升指令遵循能力，为什么不直接使用 SFT 就完事了，非要加入 RL训练呢？

这是因为 SFT 训练大模型容易导致过拟合，以数学推理任务为例，SFT 会直接强迫模型输出分布与标准解题过程一致，这可能导致模型仅学会了 “模仿” 解题过程的输出风格，但没有学会真正的数学解题能力。

另一方面，SFT 训练并非渐进式的，以数学推理任务为例，训练初期，若训练样本中包含难度较高的数学问答样本，模型因推理能力有限，会倾向去 “背题（memorize）” 而非 “理解题目”，这类样本产生的梯度会严重损害模型泛化能力；

反观 RL 训练，使用渐进学习策略，训练样本通过模型采样生成，这能保证训练样本 (prompt + response) 与模型分布间差距不大，模型能理解当前能力所及的题目，而不是去 “背题”。

具象一点说，SFT 更像是老师给学生“灌输”知识，学生能在短时间内学会一套解题套路，但模型尚未将这些知识完全内化成能力。RL 则更像是学生在老师布置的题库上不断做题、订正和反思：解题方法是模型自己采样出来的，分布始终贴着模型当前能力，从而在“做题—反馈—调整”的循环中，逐步把知识沉淀为真正的能力。

下面我将按照技术发展脉络，依序介绍大模型主流强化学习方法。从最早的 PPO 出发，依次经过 GRPO、DAPO、GSPO，再到最新的 SAPO，每一个方法都在前一代技术的基础上改进与演化。

PPO (Proximal Policy Optimization)

旧策略采样 + clip 约束的新策略更新

PPO 是经典的强化学习算法，通过旧策略采样轨迹来估计新策略的梯度，这种方法必须保证新、旧策略分布差距不大，否则，估计新策略的梯度会失准，会使用hard-clipping技巧，避免新、旧策略分布差距过大，PPO公式如下：

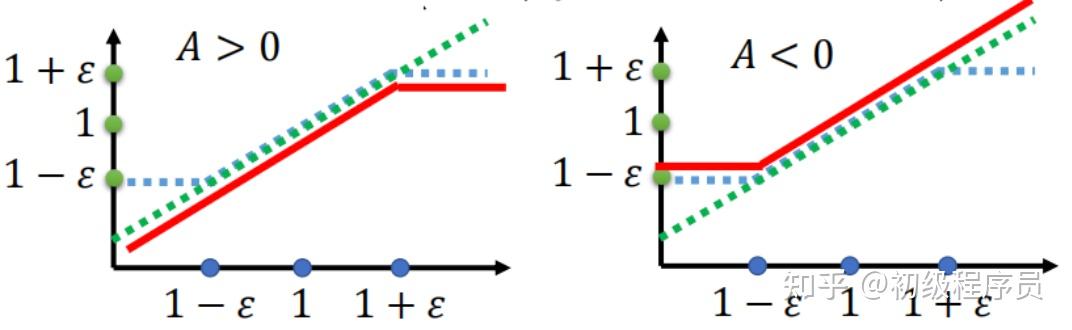
\begin{aligned} \mathcal{J}_{\mathrm{PPO}}(\theta) &= \mathbb{E}_{(q,a)\sim \mathcal{D},\, o_{\le t}\sim \pi_{\theta_{\mathrm{old}}}} \left[\, f_t \,\right], \\[4pt] f_t &= \min\!\left( \frac{\pi_{\theta}(o_t\,|\,q,o_{<t})}{\pi_{\theta_{\mathrm{old}}}(o_t\,|\,q,o_{<t})}\,\hat{A}_t,\;\; \operatorname{clip}\!\left( \frac{\pi_{\theta}(o_t\,|\,q,o_{<t})}{\pi_{\theta_{\mathrm{old}}}(o_t\,|\,q,o_{<t})}, 1-\varepsilon,\, 1+\varepsilon \right)\hat{A}_t \right) \end{aligned}

其中， \hat{A}_t 为序列的Advantage；\pi_{\theta}, \pi_{\theta_{\text{old}}} 分别为新、旧策略。 f_t 随 importance ratio \frac{\pi_{\theta}(o_t \mid q, o_{<t})}{\pi_{\theta_{\mathrm{old}}}(o_t \mid q, o_{<t})} 的变化如下图

当 \text{Advantage}>0 时，策略梯度会迫使 importance ratio变大，即提高当前token类别的输出概率。当 importance ratio 大于 1+\epsilon 时，策略梯度为0，避免新、旧策略分布差异过大； \text{Advantage}<0 时，同理可推。

PPO 训练流程如下：

1、采样轨迹 (Rollout)：通过模型生成当前批次 prompt 的 response；
2、奖励计算 (Reward)：对生成的 response 进行 sequence-level reward 计算（可通过 Reward model 预测或基于规则的方式计算奖励）；
3、计算Value：Value Model 估计每个response token的价值 (Value)，即截止到当前response token，未来生成完整个response的期望奖励回报估计；
4、计算token-level advantage：通过 GAE (Generalized Advantage Estimation，算法如下) 分配 advantage 给每个 token，形成 token-level 的监督信号；

\begin{align} \delta_t = r_t + \gamma V(s_{t+1}) - V(s_t), \quad \hat{A}_t = \sum_{l=0}^{\infty} (\gamma \lambda)^l \, \delta_{t+l}. \end{align}

5、Value Model 梯度更新；
6、策略梯度更新。

GRPO (Group Relative Policy Optimization)

丢掉 Value Model，通过采样同一 prompt 下的样本组来估计 advantage

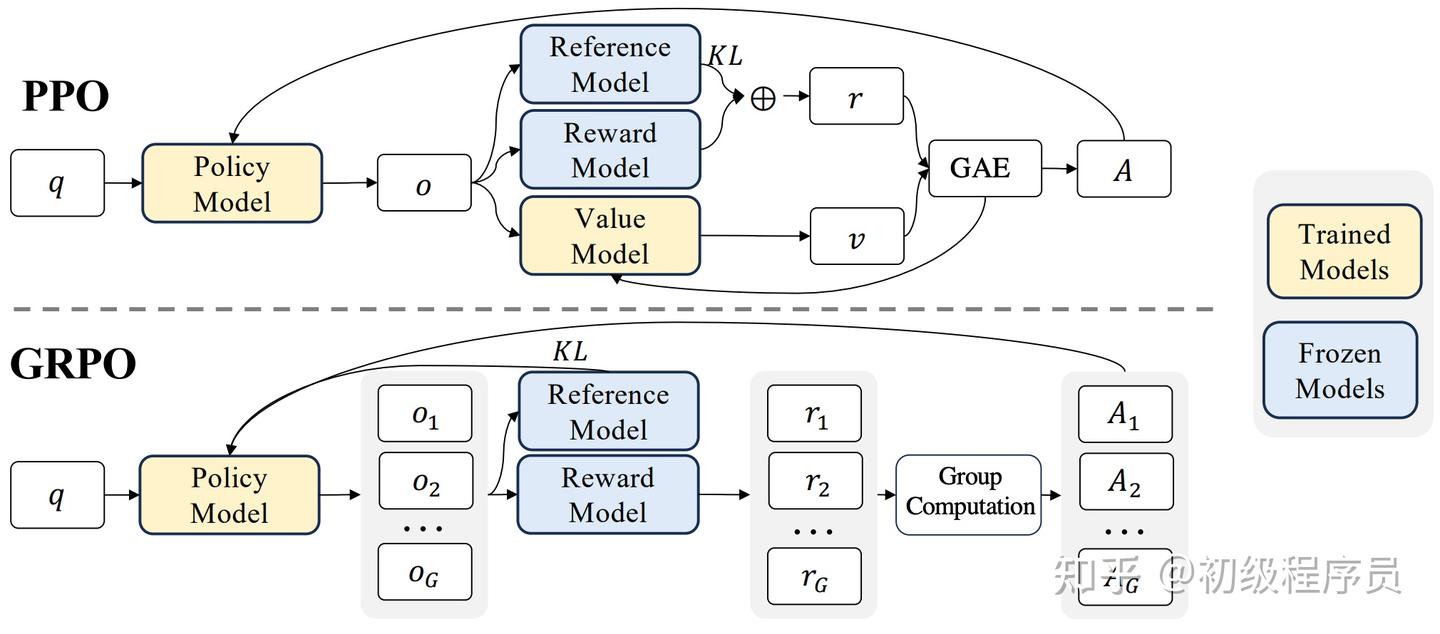
PPO与GRPO的对比，GRPO舍弃了Value Model，通过采样来估计 empirical-based advantage，降低资源开销。

PPO 存在以下几点缺点：

1、需同时训练 Value Model，造成额外计算与资源开销；
2、Advantage 估计依赖 Value Model，导致训练稳定性受到影响：PPO 的 token-level advantage 估计来自 Value Model 的预测值，因此，Value Model 的训练品质会直接影响 advantage 的准确性。

一旦 Value Model 的估计不稳定，就会使得策略模型训练变得高度不稳定。

GRPO 巧妙避开Value Model的估计，其核心想法是通过多次轨迹采样来估计 advantage。

给定一条prompt，GRPO算法会采样该条 prompt 的 G 条轨迹 \{ o_1, o_2, \ldots, o_G \} ，并计算对应的奖励 r=\{ r_1, r_2, \cdots, r_G \} ，GRPO 直接使用

empirical-based advantage \hat{A}_i = \frac{r_i - \operatorname{mean}(r)}{\operatorname{std}(r)}

(这个advantage会平均分配给response的每个token)。

GRPO 的目标函数如下：

\begin{align} \mathcal{J}_{\mathrm{GRPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\, \{o_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot\,|\,q)} \left[ \frac{1}{G} \sum_{i=1}^{G} \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left( \min\!\left( r_{i,t}(\theta)\,\hat{A}_{i}, \operatorname{clip}\!\left( r_{i,t}(\theta),\, 1-\varepsilon,\, 1+\varepsilon \right)\hat{A}_{i} \right) - \beta D_{\mathrm{KL}}\!\left( \pi_{\theta} \,\|\, \pi_{\mathrm{ref}} \right) \right) \right] \end{align}

GRPO 保留了 KL divergence项，避免模型因reward hacking导致模型崩塌。

DAPO (Dynamic Sampling Policy Optimization)

在 GRPO 的框架上，通过不对称 clip、动态采样、token-level loss 等技巧缓解训练效率和稳定性问题

DAPO是字节跳动提出针对GRPO的一系列改进方法，分为以下几个方面：

Clip Higher

GRPO存在Entropy Collapse问题，即训练早期模型输出分布的Entropy快速下降，这会抑制模型探索能力 (exploration) ，导致empirical-based advantage计算为0，降低训练效率。Entropy Collapse源于GRPO的 clip 设计：

考虑 \text{Advantage} > 0 情况，由于PPO算法只会在 \frac{\pi_{\theta}(o_t \mid q, o_{<t})}{\pi_{\theta_{\mathrm{old}}}(o_t \mid q, o_{<t})} \leq 1+\epsilon 情况下，才会提高 \pi_{\theta}(o_t \mid q, o_{<t}) 的概率，因此，当 \pi_{\theta_{\mathrm{old}}}(o_t \mid q, o_{<t}) 接近 0 时， \pi_{\theta}(o_t \mid q, o_{<t}) 提升幅度十分有限；

相反，若 \pi_{\theta_{\mathrm{old}}}(o_t \mid q, o_{<t})4 较大， \pi_{\theta}(o_t \mid q, o_{<t}) 提升幅度将相当可观，结果就是：原本概率大的 token 反而越容易被进一步放大，而那些原本概率很小但 advantage 为正的 token 几乎得不到提升，从而明显削弱了模型的探索能力。通过提高 clip 的上界，有效缓解了 Entropy Collapse 的发生。

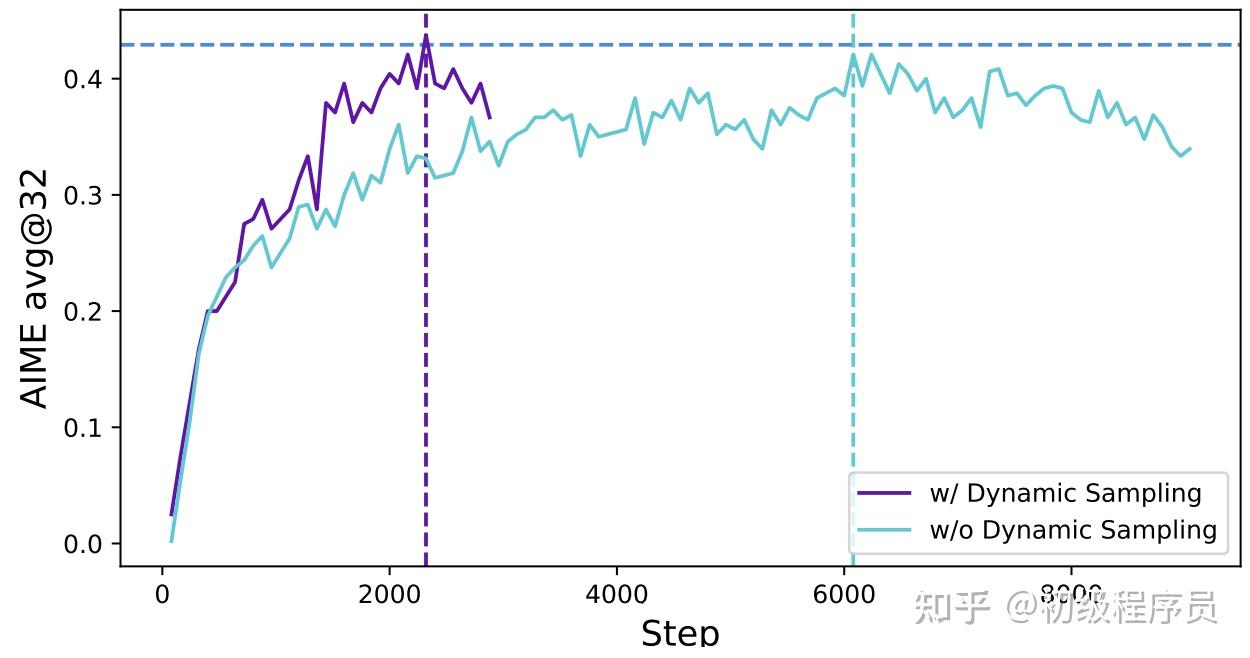
Dynamic Sampling

GRPO存在训练效率低的问题，主要原因是模型看到太简单（全对）或太难（全错）的样本，以至于采样出来的轨迹advantage全为0，没有策略梯度，因此，训练过程会滤除全对或全错的样本。

\begin{align} &\mathcal{J}_{\mathrm{DAPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\,\{o_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot \mid q)} \left[ \frac{1}{\sum_{i=1}^G |o_i|} \sum_{i=1}^G \sum_{t=1}^{|o_i|} \min\!\Big( r_{i,t}(\theta)\,\hat{A}_{i,t},\; \operatorname{clip}\big( r_{i,t}(\theta),\; 1-\varepsilon_{\mathrm{low}},\; 1+\varepsilon_{\mathrm{high}} \big)\hat{A}_{i,t} \Big) \right] \\ &\text{s.t.}\quad \color{red}{ 0 < \bigl|\{\,o_i \mid \texttt{is_equivalent}(a, o_i)\,\}\bigr| < G. } \end{align}

Token-Level Policy Gradient Loss

GRPO训练会将sequence-level advantage平均分配给每个response token，这导致长推理序列中，每个response token被分配到的advantage相当少，策略梯度强度非常弱。

因此，论文提出Token-Level Policy Gradient Loss，让同个mini-batch内，每个response token的advantage权重相同。

\begin{align} &\mathcal{J}_{\mathrm{DAPO}}(\theta) = \mathbb{E}_{(q,a)\sim\mathcal{D},\,\{o_i\}_{i=1}^G \sim \pi_{\theta_{\mathrm{old}}}(\cdot \mid q)} \left[ \frac{1}{ \color{red}{ \sum_{i=1}^G |o_i| } } \color{red}{ \sum_{i=1}^G \sum_{t=1}^{|o_i|} } \min\!\Big( r_{i,t}(\theta)\,\hat{A}_{i,t},\; \operatorname{clip}\!\big( r_{i,t}(\theta),\; 1-\varepsilon_{\mathrm{low}},\; 1+\varepsilon_{\mathrm{high}} \big)\hat{A}_{i,t} \Big) \right], \\ &\text{s.t.}\quad 0 < \bigl| \color{red}{\{o_i \mid \texttt{is_equivalent}(a,o_i)\}} \bigr| < G. \end{align}

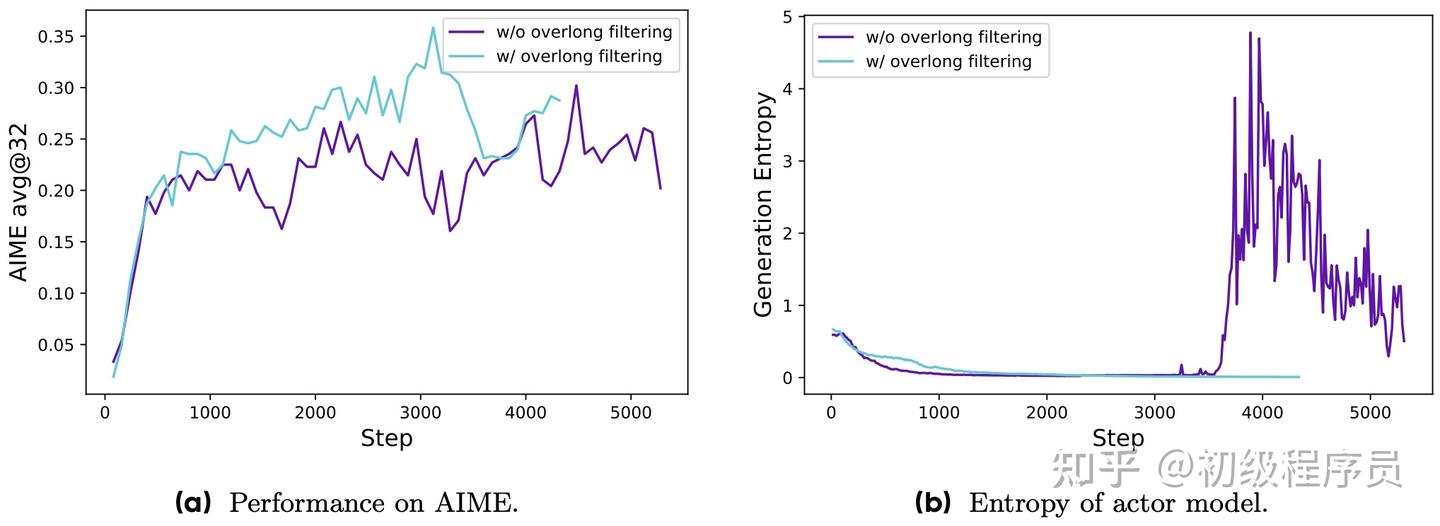
Overlong Reward Shaping

传统方法会将过长的 response 截断，这些被截断的样本也会参与到奖励计算，造成 reward noise，导致训练不稳定，通过超长过滤策略 (Overlong Filtering)，对被截断的样本进行 loss 屏蔽，提高训练稳定性。

另外，为避免模型生成过长的response，会在原有奖励基础上，加入length-aware penalty (公式如下)，惩罚长度过长的样本：

R_{\text{length}}(y) = \begin{cases} 0, & |y| \le L_{\max} - L_{\text{cache}}, \\[6pt] \dfrac{(L_{\max} - L_{\text{cache}}) - |y|}{L_{\text{cache}}}, & L_{\max} - L_{\text{cache}} < |y| \le L_{\max}, \\[10pt] -1, & L_{\max} < |y| \end{cases}

Qwen2.5-32B模型微调后在AIME测试集上准确率，以及在 RL 训练过程中【采用/未采用】Clip-Higher 策略时，模型生成概率的entropy变化。

Qwen2.5-32B模型微调后在AIME测试集上准确率，以及其生成概率的entropy变化，对比【采用/未采用】Overlong Reward Shaping策略的情况。

【采用/未采用】Dynamic Sampling 策略的对比。

GSPO (Group Sequence Policy Optimization)

把 importance ratio 提升到 sequence 级别，在 MoE 模型上能明显提升稳定性

GSPO是阿里巴巴提出针对GRPO 训练不稳定且效率低的改善方法，GSPO 将token级别的advantage与importance ratio改为sequence级别，GSPO中，sequence-level important ratio 定义为：

s_i(\theta) = \left( \frac{\pi_{\theta}(y_i \mid x)}{\pi_{\theta_{\mathrm{old}}}(y_i \mid x)} \right)^{\frac{1}{|y_i|}} = \exp\!\left( \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} \log \frac{ \pi_{\theta}(y_{i,t} \mid x, y_{i,<t}) }{ \pi_{\theta_{\mathrm{old}}}(y_{i,t} \mid x, y_{i,<t}) } \right)

目标函数为：

\mathcal{J}_{\mathrm{GSPO}}(\theta) = \mathbb{E}_{x \sim \mathcal{D},\, \{y_i\}_{i=1}^{G} \sim \pi_{\theta_{\mathrm{old}}}(\cdot \mid x)} \left[ \frac{1}{G} \sum_{i=1}^{G} \min\!\left( s_i(\theta)\,\hat{A}_i,\, \operatorname{clip}\!\left(s_i(\theta),\, 1-\varepsilon,\, 1+\varepsilon \right)\hat{A}_i \right) \right]

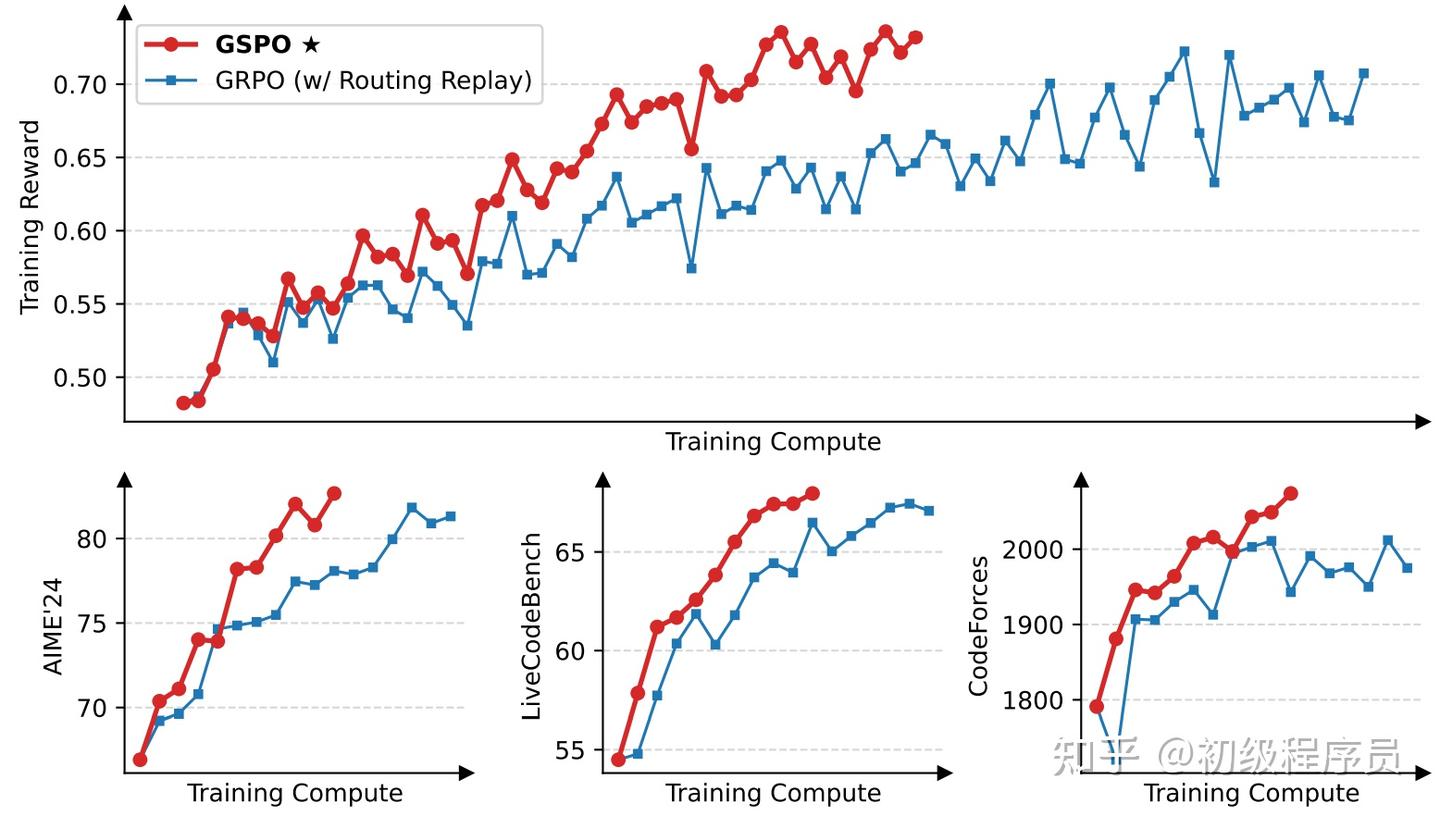
下面简短说明GSPO为什么比 GRPO更有优势：

梯度更稳定

GRPO与GSPO的策略梯度公式如下，可以明显看到，GRPO的策略梯度方向受到了 importance ratio 的扭曲，这会影响策略梯度更新的稳定性与效率，反观GSPO每个token的策略梯度权重相等，importance ratio仅决定策略梯度的强弱，不决定方向。

\begin{align} &\nabla J_{\text{GSPO}} \propto A_i \cdot (\frac{\pi_\theta(y_i)}{\pi_{\theta_{\text{old}}}(y_i)})^{1/T} \sum_{t=1}^T \nabla \log p_{i,t} \\ &\nabla J_{\text{GRPO}} \propto A_i \cdot \sum_{t=1}^T \frac{\pi_\theta(y_{i,t})}{\pi_{\theta_{\text{old}}}(y_{i,t})} \nabla \log p_{i,t} \end{align}

MOE训练更稳定

MoE 模型训练难度大，每次策略梯度更新都可能改变激活的专家，从而导致同个序列的 token-level importance ratio 出现剧烈震荡，阻碍模型有效收敛。论文以微调 Qwen3-30B-A3B-Base 为例，每次策略梯度更新平均会激活约 10% 的新专家。

GSPO 通过约束 sequence-level importance ratio，在 MoE 训练会更具优势，因为后训练阶段，MoE 的每个专家都具备一定的语言建模能力，这保证了即使 token-level importance ratio 波动剧烈，整体的 sequence-level importance ratio 仍能保持相对稳定，因此 GSPO 更有利于MoE 模型训练的效率与稳定性。

由 Qwen3-30B-A3B-Base 冷启动微调所得模型的训练曲线。 GSPO 的训练效率明显高于 GRPO。

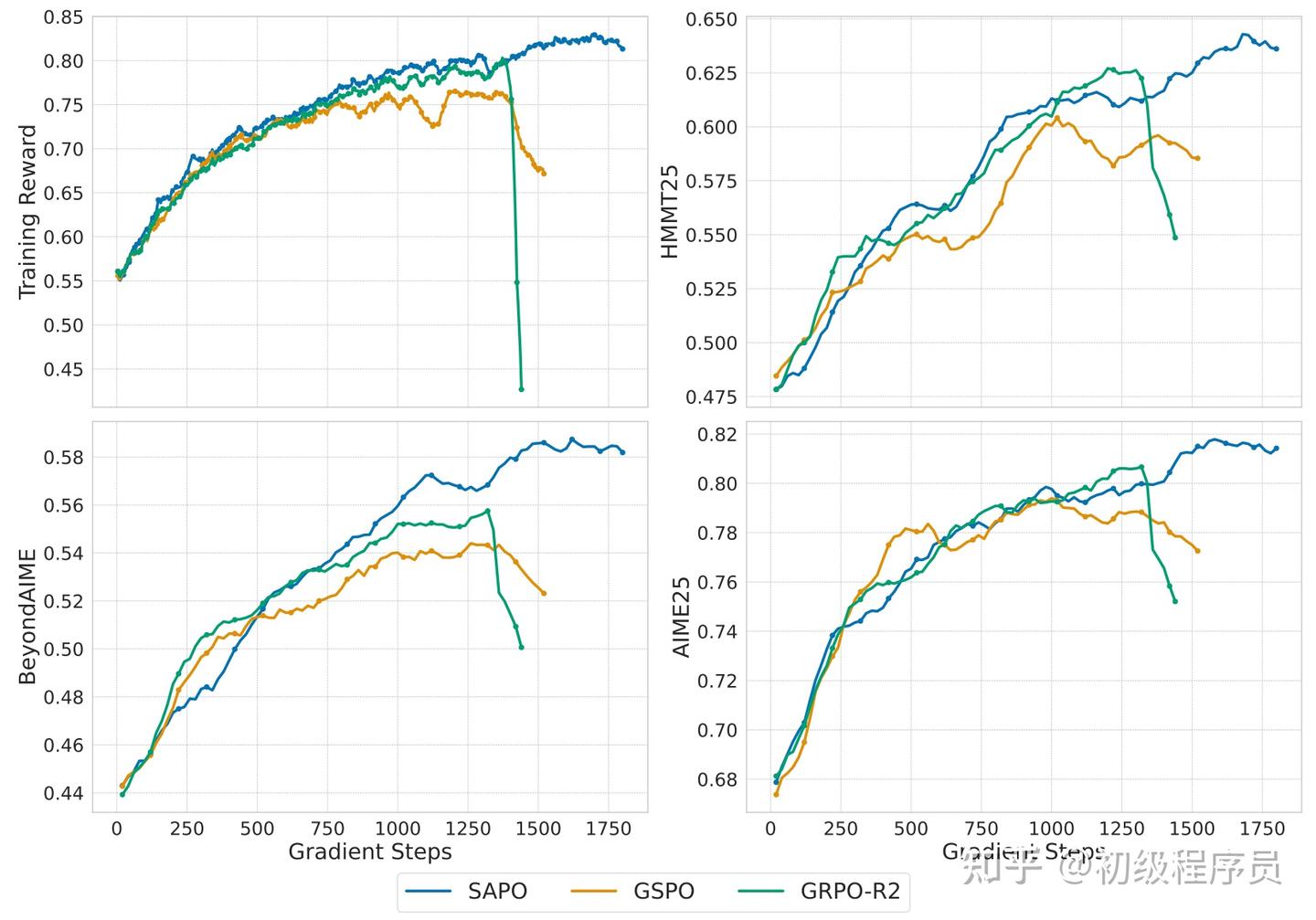
SAPO (Soft Adaptive Policy Optimization)

用 soft gate 代替硬 clip，在 GSPO 与 GRPO 之间连续平滑过渡，兼顾稳定性与效率

SAPO对GSPO做了进一步优化，GSPO使用sequence-level hard-clipping机制，这导致部分序列因sequence-level importance ratio过大，而被clip掉，以致整条序列的策略梯度为 0，影响训练效率。

SAPO将hard-clipping改为soft gate函数 f_{i,t}(x) ，避免了策略梯度为 0 的问题。SAPO目标函数为：

\mathcal{J}(\theta) = \mathbb{E}_{q \sim \mathcal{D},\, \{y_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(\cdot \mid q)} \left[ \frac{1}{G} \sum_{i=1}^G \frac{1}{|y_i|} \sum_{t=1}^{|y_i|} f_{i,t}(r_{i,t}(\theta)) \, \hat{A}_{i,t} \right]

其中

f_{i,t}(x) = \sigma\!\left( \tau_{i,t}(x-1) \right) \cdot \frac{4}{\tau_{i,t}}, \qquad \tau_{i,t} = \begin{cases} \tau_{\text{pos}}, & \hat{A}_{i,t} > 0, \\[4pt] \tau_{\text{neg}}, & \text{otherwise.} \end{cases}

\sigma 为sigmoid函数。

SAPO的策略梯度为：

\begin{align} &\nabla J_{\text{SAPO}} \propto \sum_{t=1}^{T} w_{i,t}(\theta)\, r_{i,t}(\theta)\, \nabla \log p_{i,t}, \\ &w_{i,t}(\theta) = 4\, p_{i,t}(\theta)\bigl(1 - p_{i,t}(\theta)\bigr), \qquad p_{i,t}(\theta) = \sigma\!\bigl(\tau_{i,t}\bigl(r_{i,t}(\theta) - 1\bigr)\bigr) \end{align}

右下图为 \text{Advantage} > 0 情况下，importance ratio r_{i,t} 与 w_{i,t} 间的变化，结合SAPO策略梯度公式可观察：

策略梯度强度随着 r_{i,t}(\theta) 远离 1 ，呈现平滑递减，对比hard-clipping方法，在 r_{i,t}(\theta)>1+\epsilon 时，策略梯度直接为 0；
随着温度 \tau 上升，策略梯度递减速度增加，SAPO使用不同的 \tau_{\text{pos}}, \tau_{\text{neg}} 其实在控制 positive / negative advantage token 的策略梯度强度；

![advantage0 情况下的比较。左图展示目标函数随 importance ratio 的变化曲线；右图展示对应的梯度权重随 importance ratio 变化的曲线。" />

总结来说，SAPO有两个主要创新点：

soft gate 取代 hard-clipping：提高训练稳定性与效率；
正负token非对称温度 (\tau_{\text{pos}} \text{/} \tau_{\text{neg}})：由于 negative advantage token 倾向提高所有非当前token类别概率，导致许多无关token类别概率增加，引发训练不稳定，因此，设定 \tau_{\text{neg}} > \tau_{\text{pos}} 旨在降低negative advantage token的影响，提高训练稳定性。

SAPO同时具有GSPO与GRPO的优势，论文证明当轨迹满足以下条件：

(A1) Small-step/on-policy：要求 token-level importance ratio r_{i,t}(\theta)\approx 1 ；

(A2) 序列内低离散性：令

z_{i,t}(\theta) := \log r_{i,t}(\theta) ， \mu_i(\theta) := \frac{1}{|y_i|}\sum_t z_{i,t}(\theta) = \log s_i(\theta)

要求

\mathrm{Var}_i(\theta) := \frac{1}{|y_i|}\sum_t \left(z_{i,t}(\theta) - \mu_i(\theta)\right)^2

很小。

SAPO可近似为smooth gate版本的 GSPO

\begin{align} \nabla_\theta \mathcal{J}_{\mathrm{SAPO}} \approx \mathbb{E} [\frac{1}{G} \sum_{i=1}^G \operatorname{sech}^2\!\left( \frac{\tau_i}{2} \log s_i(\theta) \right)\, \nabla_\theta \log s_i(\theta)\, \hat{A}_i ], \quad s_i(\theta) = \left( \frac{\pi_{\theta}(y_i \mid x)}{\pi_{\theta_{\mathrm{old}}}(y_i \mid x)} \right)^{\frac{1}{|y_i|}} \end{align}

因此，SAPO 同时具有 sequence-level 与 token-level 特性。在 (A1)–(A2) 条件满足时，其目标函数与 GSPO 相近；而在条件不满足时，其行为退化为 GRPO。

同时，SAPO 通过 soft gate 在 on-policy 与 off-policy 策略间进行连续化的权重调整，以避免硬式切换造成的非平滑策略梯度，从而增强整个优化过程的稳定性。

对 Qwen3-30BA3B-Base 模型进行不同 RL 方法下的训练与验证表现。 SAPO 的学习过程始终稳定，最终性能也更高；相比之下，GSPO 与 GRPO-R2 都在训练早期出现崩塌现象。

总结

PPO, GRPO, DAPO, GSPO, SAPO 可以视作一条面向大模型强化学习微调的算法演进链：PPO 作为经典强化学习算法，在旧策略采样、clip 约束小步更新的框架下，让大模型可以稳定做策略梯度；

GRPO 通过同一 prompt 下的样本组来估计 empirical advantage，省去了 Value Model 的训练开销；

DAPO 在 GRPO 的基础上加入不对称 clip、动态采样、token-level policy loss 与长度奖励等技术，显著提升长推理序列的训练效率与稳定性；

GSPO 将 importance ratio 与 advantage 提升到 sequence 级别，缓解 MoE 等大模型训练中token-level importance ratio剧烈波动带来的不稳定；

在此之上，SAPO 以 soft gate 取代 hard-clipping，并通过正负 advantage 不同温度，在 sequence-level 与 token-level、on-policy 与 off-policy 之间实现自适应折中，兼顾了训练稳定性与效率。