作者：小红师兄

https://zhuanlan.zhihu.com/p/1980358735869268796

今天聊聊AdaMoE(VLA)，先用一句话概括一下：AdaMoE 这篇论文想解决的是「在 Vision-Language-Action (VLA) 模型里用 Mixture-of-Experts（MoE）扩容时，路由器既要负载均衡、又要让专家真正各司其职，这两个目标经常互相打架」的问题。

作者的核心观点是：“专家不需要垄断舞台（expertise need not monopolize）”——也就是说，不需要某一个专家一旦被选中，就在输出里占据绝对话语权；选择哪些专家、以及这些专家贡献多大权重，这两件事本来就不该绑死在一起。

背景

VLA 模型（OpenVLA、π0 等）已经在机器人操作任务上做得不错，可以把视觉、语言和动作统一在一个端到端框架里。

在大规模 Vision-Language 模型里，MoE 是非常成熟的一种扩容方式，比如 MoE-LLaVA、DeepSeek-VL2、Kimi-VL 等，它们都靠稀疏专家带来更强能力、但推理开销基本不涨。

机器人这边也很自然想：能不能把已有的 VLA 基座模型（比如 π0）改造成 MoE，一方面继承原来的知识，另一方面靠 MoE 扩容、提高性能、还保持推理成本可控？

问题在于：机器人操作里的 MoE 路由，比起纯语言任务更容易「翻车」。作者的发现是：

• 负载均衡（load balancing）如果太强，会损伤任务性能；
• 负载均衡如果太弱，又会出现 expert collapse：大部分 token 都流向少数专家，其它专家几乎不工作；
• 本质上，负载均衡损失希望专家使用得平均一些，而任务目标其实希望专家高度「偏心」——不同任务、不同操作场景，本来就该让少数专家主导决策。

在传统 MoE 架构里，这两个目标是通过同一套 router logits 来优化的，结果就是：

router 同时要负责：1）选谁上场；2）每个人贡献多少。

这两个目标对 logits 的要求又是互相冲突的，训练就容易收敛到一个谁都不太满意的「折中」。

AdaMoE 的核心就是：

• 继续用 MoE 来扩 π0 的 action expert；
• 但在路由层面，把「选专家」和「给权重」这两件事解耦，用一个额外的 scale adapter 专门负责「贡献多大」。

下面用一个小例子来理解这件事：

想象一个桌面整理机器人，任务指令是「把桌面上的蓝色杯子收进右侧的收纳盒」。

• 它需要看多视角相机画面，理解语言指令；
• 然后输出一段动作序列：靠近杯子 → 抓稳 → 抬起 → 平移到盒子上方 → 放下。

这些操作里，看上去都叫「整理桌面」，但所需的微操技能其实挺多样：抓握、避障、细腻放置……各个专家就像不同风格的「抓杯子/移动/放置」专家。 AdaMoE 想做的是：既要让多位专家上场协作，又不要让某一个人永远抢戏、其他人长期闲置。

AdaMoE 做了哪些设计？

按照论文的结构，方法部分主要有三块：

• 在 π0 的框架下，用条件流匹配（conditional flow matching）来建模机器人动作分布；
• 在 π0 的 action expert 里引入一个 MoE 架构，分为 shared experts 和 routed experts，并配套负载均衡 loss；
• 针对传统 MoE 中「选择 = 权重」的耦合问题，引入 scale adapter，把专家选择和权重解耦。

对应到我们的「桌面整理机器人」例子：

• 整体上还是用 π0 那套「从噪声开始、逐步去噪」的流匹配方式，去生成一整段高频控制动作；
• 原本 π0 里负责「理解当前动作 token 该怎么变好」的那一块 action expert，现在被换成了带 MoE 的版本：有专门做通用动作的 shared expert，也有专门负责某些动作模式（比如抓、放、横移）的 routed experts；
• 为了不让 router 又要负责平衡使用率、又要负责谁该更重要，作者额外加了一个结构一致的 scale adapter，专门调节专家的贡献强度。

模型架构细节

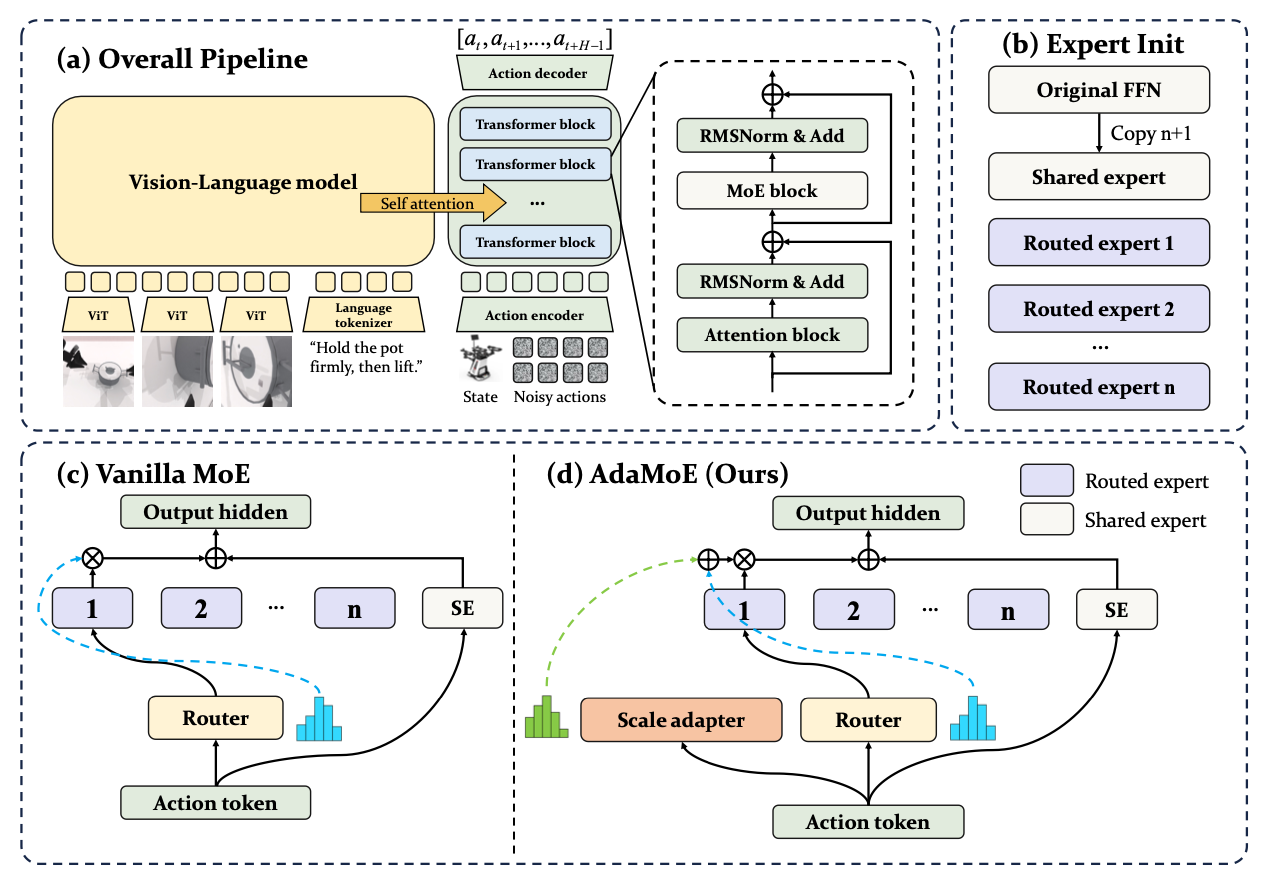
Problem formulation：条件流匹配下的控制问题

AdaMoE 是在一个已经训练好的 VLA 基座模型 π0 上做 MoE 扩展的。π0 本身是一个基于 flow matching 的 VLA 模型，用来做高频率的动作控制。

在每个时间步 t，模型接收一个观测 \mathbf{O}_t，里面包括：

• 多视角的 RGB 图像；
• 一条语言指令；
• 机器人本体状态（关节角度、夹爪状态等）。

论文中写的是：

• 观测： ​\mathbf{O}_t = [\mathbf{I}_1^t,\ldots,\mathbf{I}_n^t, \ell_t, \mathbf{q}_t]，其中 ​\mathbf{I}_i^t 是第 ​i 个相机在时刻 ​t 拍到的图像，​\ell_t 是自然语言指令，​\mathbf{q}_t 是机器人的本体状态（proprioceptive state）。
• 动作 chunk： ​\mathbf{A}_t = [a_t, a_{t+1}, \ldots, a_{t+H-1}]
  表示未来 ​H 步的高频动作序列。

控制问题就是学习一个条件分布 ​\pi(\mathbf{A}_t \mid \mathbf{O}_t) ，让机器人根据当前观测，输出一整段未来动作。

在桌面整理的例子里：

• ​\mathbf{O}_t 里包含多视角的桌面图像和一句「把蓝色杯子放进右侧收纳盒」；
• ​\mathbf{A}_t 就是一小段「从当前时刻开始往后」的动作，比如连续 10 步控制：移动手臂、闭合夹爪、抬起、平移、张开夹爪……

论文用的是 条件流匹配（conditional flow matching） 来建模这个分布。关键量包括：

• 把真实动作 chunk ​\mathbf{A}_t 和一个高斯噪声向量 ​{\epsilon} \sim \mathcal{N}(0, I) 线性插值： ​\mathbf{A}_t^{\tau} = (1 - \tau)\mathbf{A}_t + \tau {\epsilon} ,其中 ​\tau \in [0, 1] 是「噪声时间」。
• 定义目标速度场： ​\mathbf{u}(\mathbf{A}_t^{\tau} \mid \mathbf{A}_t) = {\epsilon} - \mathbf{A}_t.

训练的时候，通过 flow matching loss 让模型学会从带噪动作 ​\mathbf{A}_t^{\tau} 、观测 ​\mathbf{O}_t 预测出这个「去噪方向」。推理时：

• 从纯噪声开始：​\mathbf{A}_t^1 \sim \mathcal{N}(0,I) ；
• 把 [0,1] 划成 N 个小步，步长 ​d\tau = 1/N ；
• 迭代应用一个基于学习得到的速度场 ​\mathbf{v}_\theta(\mathbf{A}_t^{\tau}, \mathbf{O}_t) 的去噪更新，直到得到 ​\mathbf{A}_t^0 作为最终动作预测。

直观一点说：

• 把「生成一段动作」这件事，拆成「从纯噪声慢慢往好动作挪」的过程；
• 在每个噪声时间点 ​\tau ，模型都要学会：在当前观测 ​\mathbf{O}_t 下，这个带噪动作 ​\mathbf{A}_t^{\tau} 应该往哪个方向移动，才能更接近真实的 ​\mathbf{A}_t 。

在桌面整理例子里，可以理解成：

• 一开始，模型「脑子里想象」的动作序列是纯随机乱动的手臂轨迹；
• 经过很多小步迭代，每一步都让它根据桌面图像和指令，去掉一点噪声、加一点有意义的动作模式，最后变成「稳稳抓起蓝色杯子并放入盒子」的那条轨迹。

AdaMoE 在这个框架下做的事情是：不改输入输出形式，也不改 flow matching 目标，只是在内部把负责处理动作 token 的子模块换成了 MoE 版。也就是下面要讲的 MoE-Architecture。

MoE-Architecture：在 π0 的动作专家里插入 MoE

作者是在 π0 的 action expert 模块内部插入 MoE，而不是整个模型都 MoE 化。论文里写得很明确：

Building upon the ​\pi_0 framework, we introduce a MoE architecture specifically within the ​\pi_0’s action expert as shown in Figure 1.

这个 MoE 动作专家由两类专家组成：

Shared experts：

• 处理所有任务里都常见的动作模式；
• 捕获「通用的操作知识」，比如常规的移动轨迹平滑、手臂基础协调等；
• 每个动作 token 都会经过 shared experts，始终处于激活状态，用来提供稳定的基础表现。

Routed experts：

• 通过学习到的 gating 机制来选择；
• 更偏向「专攻某类动作或者某类任务」；
• 不同 routed expert 可以专门适应不同类型的操控场景。

对于每个动作 ​token x_a ，MoE 动作专家的输出由两部分组成：

• 一部分来自 always-on 的 ​F_{shared}(\cdot) ；
• 一部分来自若干个被选中的路由专家 ​F_{routed}^{(i)}(\cdot) ，它们通过 gating 给出权重 ​w_i(x_a) 之后再被融合。

论文里提到的 gating 机制：

• gating 网络记作 ​G(\cdot) ；
• 对每个动作 token，它先对所有 routed experts 打分；
• 然后用 top-k selection 选出得分最高的 k 个专家，只激活这 k 个；
• 这样可以在保持表达能力的同时，维持计算成本不随专家数线性上涨。

在桌面整理的例子里，可以这样理解：

• shared experts：负责「基础动作风格」，比如通用的移动顺滑、不撞桌沿；
• routed experts：
  • 专家 1：专精「抓起桌面上的物体」；
  • 专家 2：专精「把物体放进盒子」；
  • 专家 3：专精「避开桌面上其它物体」……

当机器人正在执行「把蓝色杯子从桌面抬起」这段 token 时：

• gating 可能主要激活「抓起」相关的几个专家，再加上 shared experts；
• 到了「把杯子放进盒子」这段 token 时，又会更偏向激活「放置」相关专家；
• 这就是 MoE 在动作空间里的「按需选专家」。

负载均衡：防止专家崩塌（expert collapse）

引入 MoE 后一个经典问题是：如果 router 一直偏爱某几个专家，其他专家就几乎不被用到，模型等于白扩容了。

为此，AdaMoE 在 routed experts 上加入了一个负载均衡损失（load balancing loss），目标是：

• 在 ​top-k 路由机制下，让每个专家被选中的频率尽量均衡；
• 同时，让 gating 概率本身也不要长期倾向某几个专家。

论文中对两个核心统计量做了明确定义：

• 对于第 ​i 个专家，被选中频率：

这里 ​N 是 token 总数，​f_i 表示「在所有 token 中，第 ​i 个专家出现在 top-k 里的比例」。

• 对应的平均 gating 概率：

其中 ​g_j^{(i)} 是第 ​j 个 token 对第 ​i 个专家的 router logit，​\text{softmax}(g_j^{(i)}) 是在 softmax 之后对应的 gating 概率。

论文中引入了一个带超参数 ​\alpha 的负载均衡损失 ​\mathcal{L}_{balance} ，通过 ​f_i 和 ​p_i 来约束专家的使用频率和 gating 概率，使它们更加均衡。​\alpha 控制这个均衡约束的强度。

直观理解：

• ​f_i 看「被选中次数」；
• ​p_i 看「被分配的概率质量」；
• 负载均衡损失会惩罚「有的专家几乎从不被选、或者几乎不拿到概率权重」的情况（比如，如果某个专家在一大批 token 上几乎从不出现在 top‑k 中，那它对应的 ​f_i 会非常小；
  又或者 softmax 后的大部分概率质量长期集中在少数几个专家上，其它专家的 ​p_i 接近 0，这两种不均衡都会让 ​\mathcal{L}_{\text{balance}} 变大，因为这个 loss 本质上是在度量 ​\{f_i\}, ​\{p_i\} 和均匀分布 ​1/K 的偏离程度——谁被用得特别多或者特别少，都会把这组数往「不均匀」方向拉，偏离越大，loss 就越大。在反向传播时就会给 router 施压，让它在之后的路由中「多分一点 token 和概率」给这些冷门专家）。

在桌面整理的例子里：

• 如果 router 总是用「抓杯子」专家和「放置」专家，但基本不用「避障」专家；
• 那么 ​f_{\text{避障}} 和 ​p_{\text{避障}} 都会很小；
• 负载均衡损失会推动 router 偶尔也多用一点「避障」专家，给它机会学习属于自己那一类模式，这样将来在更复杂桌面布局上就更有用。

总的训练目标，是把原来的 flow matching loss 和这个负载均衡 loss 加在一起：

• flow matching 部分仍然主导「动作生成要贴近真实轨迹」；
• 负载均衡部分则防止专家崩塌，让所有 routed experts 都有机会逐渐学到自己擅长的子任务。

Decoupled Expert Selection and Weighting：解耦「选谁」和「权重大」

上面说的是一个「常规的 MoE 动作专家 + 负载均衡」故事。但作者发现，一个更深层的问题在于 传统 MoE 的路由机制把「选择哪个专家」和「这个专家权重多大」绑在了一起。

传统 MoE 的耦合设计

在传统 MoE 里，大致流程是：

• router 先对每个专家算一个 ​logit r_i(x)；
• 对所有 ​r_i(x) 做 softmax，得到专家概率；
• 用 ​top-k 选出概率最高的 ​k 个专家；

最后，用这同一组 softmax 概率作为加权系数，把这些专家的输出加权求和。
论文指出的问题是：

• 负载均衡损失 ​\mathcal{L}_{balance} 希望 softmax 出来的概率「看上去比较平均」，这样专家用得更均匀；
• 但任务损失 ​\mathcal{L}_\tau（这里是 flow matching 相关的主任务 loss）又希望有比较「偏心」的分布，比如在某些操作场景中，少数几个动作专家特别重要；
• 这两个目标都是通过同一组 router ​logits r_i(x) 来优化的，于是：
  • 同样一组 logits，要既负责让专家出场频率平均；
  • 又要在任务需要的时候，大幅偏向某个专家；
  • 结果就是 router 不得不在两边「折中」，不能很好地满足任何一边。

换回桌面整理的例子：

• 对于「抓起杯子」这个场景，任务损失其实希望「抓握专家」权重大一些；
• 可是负载均衡又希望所有专家长期看起来都差不多常用；
• 如果选择和权重都来自同一个 softmax，router 就会卡在中间：抓握专家既不能太突出（否则不平衡），又不能太弱（否则抓不好）。

AdaMoE 的解法：加一个 scale adapter

论文给的思路是很直接的：

把「选谁上场」和「上场之后贡献多少」这两件事拆开做。

具体做法是：

• 在原有 router ​R(\cdot) 的基础上，引入一个新的 scale ​adapterS(\cdot) ；
• 这两个模块在结构上是一样的，但承担的角色不一样：
  • router ​R(\cdot)：决定 哪些专家被选中，主要负责多样性和负载均衡；
  • scale adapter ​S(\cdot)：在专家已经被选中的前提下，调节它们在最终输出里的贡献大小，主要服务任务性能。

论文中写道：

? Our scale adapter ​S(\cdot) shares the identical architecture as the original router ​R(\cdot) but serves a distinct purpose: while the router determines which experts to select, the scale adapter additively adjusts how much each selected expert should contribute to the final output.

形式上，对于输入 ​x，

• router 会产生 ​logits R_i(x) 并通过 ​top-k 决定被选中的专家集合；
• scale adapter 会产生对应的 ​logits S_i(x) ；
• 对于被选中的专家，第 ​i 个专家的最终权重系数，来自 router 与 scale adapter 的 加和：

（论文里是描述性表述：the final weighting coefficient for each selected expert is the sum of its scale adapter contribution and its router contribution。）

这样一来，优化目标就被「分流」了：

router ​R(\cdot) 这条路更多对齐负载均衡：

• 让不同专家在不同场景下被选中的机会更均匀；
• 满足 ​\mathcal{L}_{balance} 对 ​f_i、p_i 的约束；

scale adapter ​S(\cdot) 则主要对齐任务损失：

• 在已经选中的专家集合里，根据当前具体操作场景，自由地拉高或拉低各个专家的贡献；
• 不再直接被负载均衡强行「拽回去」。

我们回到到桌面整理的例子：

router 决定：

• 「抓起杯子」动作阶段：选中「抓握专家 + 基础移动专家 + 轻微避障专家」这几个；
• 「把杯子放进盒子」阶段：选中「放置专家 + 基础移动专家 + 更强避障专家」这几个；

scale adapter 再根据当前 token 的具体状态：

• 对「抓起」阶段，把抓握专家的权重往上拉，避障专家权重可以相对小一点；
• 对「放入盒子」阶段，把放置专家和避障专家的权重拉高，抓握专家权重下降。

关键是：

• 谁被选中（由 router 决定）可以保持相对多样、平均使用，满足负载均衡，不轻易「一刀切」某些专家；
• 谁更重要（由 scale adapter 决定）则可以更大胆地「偏心」，只要对任务 loss 有好处就行，不被负载均衡直接限制。

简单来讲就是：某个专家「被选中上场」并不意味着它就该「唱主角」；它可以在场，但只在恰当的时刻、用恰当的强度出力。

实验

简单带一下论文里给的结果数量级：

• 在 LIBERO 任务上，相比 π0 基线有 1.8% 的提升；
• 在 19 个 RoboTwin「hard setting」任务上，成功率提升 9.3%；
• 在真实机器人实验中，有 21.5% 的提升。

这些数字的重点不是「涨了多少」，而是：在不推高推理计算量（top-k 稀疏激活）的前提下，通过在 action expert 里做 MoE + 解耦路由，确实能在模拟和真实场景里都带来比较稳定的收益。

对应到桌面整理机器人，可以理解为：在各种「收杯子」「避开桌面杂物」「放进不同位置的盒子」任务中，AdaMoE 让机器人更容易学到适合「抓起」「放下」「避障」等不同子技能的专家，并在推理时按需组合使用这些专家，而不是总指望一个「万能专家」。

总结

从论文本身来看，AdaMoE 做的事情比较「外科手术式」：

1、不重新设计整个 VLA，只是在 π0 的 action expert 上做 MoE 化；

2、MoE 部分也不是花样很多的 tricks，而是抓住了一个挺本质的点：

• 在机器人这类任务里，负载均衡和专家专门化确实是硬需求；
• 传统「选择 + 权重二合一」的路由机制，会让这两个目标直接在同一组 logits 上打架；
• 解耦之后，再用 scale adapter 专门调节贡献强度，会让设计更自然。

3、从「怎么用在别的 VLA 上」的角度看，这篇工作给的启发大概有几点：

• 如果已经有一个不错的 VLA 基座模型（比如 π0 一类），可以考虑优先在 action expert 这种「直接关乎控制质量」的子模块里做 MoE 扩展；不一定要全模型都 MoE 化。
• 做 MoE 时，一定要认真想清楚 router 在任务里的角色：它既是「调度专家资源」的中枢，又会直接影响专家到底学到什么样的模式；把「让谁上场」和「谁更重要」分开，往往有助于理清这些目标。
• 在机器人这样对稳定性和泛化都很敏感的场景下，单纯追求参数规模并不一定带来线性收益；像 AdaMoE 这样「架构上让专家更好协作」的设计，往往更划算。

4、如果之后打算在别的 VLA 架构上做 MoE 类似的改造，这篇论文的套路可以作为一个相对干净、可复用的模板：

• 保留原有的条件流匹配或其它动作建模方式；
• 把动作相关的核心子网络拆成 shared + routed experts；
• 用 top-k 稀疏路由 + 负载均衡 loss 防止专家崩塌；
• 再额外加一个 scale adapter，把专家选择和权重从优化目标层面「解绑」。